Giải bài tập về tính đối xứng của đường tròn
Giải bài 1 trang 99 sgk hình học 9 tập 1
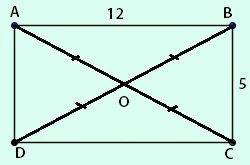
Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rẳng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Bài giải:
Gọi O là giao điểm của hai đường chéo AC, BD của hình chữ nhật ABCD. Khi đó ta có OA = OB = OC = OD
A, B, C, D cùng cách đều điểm O nên 4 điểm đó thuộc cùng một đường tròn tâm O bán kính R = OA
Áp dụng định lí Pi-ta-go trong tam giác ABC vuông tại B, ta có:
$AC^2$ = $AB^2$ + $BC^2$ = $12^2$ + $5^2$ = 144 + 25 = 169
=> AC = $\sqrt{169}$ = 13
OA = $\frac{AC}{2}$ = $\frac{13}{2}$ = 6,5
Vậy bán kính của đường tròn bằng 6,5cm
Ghi vào sổ tay: Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm đó cùng cách đều một điểm.
Bài giải:
Ghi vào sổ tay: Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm đó cùng cách đều một điểm.
Giải bài 2 trang 100 sgk hình học 9 tập 1
Hãy nối mỗi ô ở cột trái với một ô ở cột phải để được khẳng định đúng:| (1) Nếu tam giác có ba góc nhọn | (4) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên ngoài tam giác. |
| (2) Nếu tam giác có góc vuông | (5) thì tâm của đường tròn ngoại tiếp tam giác đó nằm bên trong tam giác. |
(3) Nếu tam giác có góc tù
|
(6) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh lớn nhất. |
| (7) thì tâm của đường tròn ngoại tiếp tam giác đó là trung điểm của cạnh nhỏ nhất. |
- Nếu tam giác có ba góc nhọn, ta có hình vẽ sau:
Như vậy sẽ nối (1) với (5)
- Nếu tam giác có góc vuông, ta có hình vẽ sau:
Khi đó ta sẽ nối (2) với (6)
- Nếu tam giác có góc tù, ta có hình vẽ sau:
Rõ ràng phải nối (3) với (4)
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Bài giải:
a) Giả sử tam giác ABC vuông tại A, với O là trung điểm cạnh huyền BC, ta có:
Đường trung tuyến AO = $\frac{1}{2}$.BC <=> OA = OB = OC
Do đó O chính là tâm của đường tròn ngoại tiếp tam giác ABC.
b) Giả sử tam giác ABC nội tiếp đường tròn tâm O, đường kính BC
Khi đó ta có OA, OB, OC là các bán kính của đường tròn.
Suy ra OA = OB = OC = $\frac{1}{2}$.BC
Vậy tam giác ABC có trung tuyến AO bằng một nửa cạnh đối diện BC nên ABC là tam giác vuông.
Ghi vào sổ tay: Ghi nhớ các định lí trên để vận dụng giải các bài tập về nhận biết tam giác vuông.
Bài giải:
Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ như hình vẽ bên, ta có:
$OA^2$ = $x^2_A$ + $y^2_A$ = $(-1)^2$ + $(-1)^2$ = 2
=> OA = $\sqrt{2}$ < R
Do đó A nằm trong đường tròn (O ; 2)
$OB^2$ = $x^2_B$ + $y^2_B$ = $(-1)^2$ + $(-2)^2$ = 5
=> OB = $\sqrt{5}$ > R
Do đó B nằm ngoài đường tròn (O ; 2)
$OC^2$ = $x^2_C$ + $y^2_C$ = $(\sqrt{2})^2$ + $(\sqrt{2})^2$ = 4
=> OC = $\sqrt{4}$ = 2 = R
Do đó C nằm trên đường tròn (O ; 2)
Bài giải:
- Gấp tấm bìa sao cho hai nửa đường tròn trùng khít lên nhau. Nếp gấp là một đường kính của đường tròn.
- Tương tự như vậy, gấp tấm bìa theo một nếp gấp khác, ta được đường kính thứ hai.
Giao điểm của hai đường kính đó chính là tâm của đường tròn.
Hoặc có thể làm theo cách:
- Lấy ba điểm A, B, C phân biệt trên đường tròn
- Nối A với B, A với C
- Dựng đường trung trực của AB, AC.
Hai đường trung trực này cắt nhau tại O. Đó chính là tâm của đường tròn.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài 3 trang 100 sgk hình học 9 tập 1
Chứng minh định lí sau:a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.
Bài giải:
a) Giả sử tam giác ABC vuông tại A, với O là trung điểm cạnh huyền BC, ta có:
Đường trung tuyến AO = $\frac{1}{2}$.BC <=> OA = OB = OC
Do đó O chính là tâm của đường tròn ngoại tiếp tam giác ABC.
b) Giả sử tam giác ABC nội tiếp đường tròn tâm O, đường kính BC
Khi đó ta có OA, OB, OC là các bán kính của đường tròn.
Suy ra OA = OB = OC = $\frac{1}{2}$.BC
Vậy tam giác ABC có trung tuyến AO bằng một nửa cạnh đối diện BC nên ABC là tam giác vuông.
Ghi vào sổ tay: Ghi nhớ các định lí trên để vận dụng giải các bài tập về nhận biết tam giác vuông.
Giải bài 4 trang 100 sgk hình học 9 tập 1
Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(-1; -1), B(-1; -2), C($\sqrt{2}$; $\sqrt{2}$) đối với đường tròn tâm O bán kính 2.Bài giải:
Biểu diễn các điểm A, B, C trên mặt phẳng tọa độ như hình vẽ bên, ta có:
$OA^2$ = $x^2_A$ + $y^2_A$ = $(-1)^2$ + $(-1)^2$ = 2
=> OA = $\sqrt{2}$ < R
Do đó A nằm trong đường tròn (O ; 2)
$OB^2$ = $x^2_B$ + $y^2_B$ = $(-1)^2$ + $(-2)^2$ = 5
=> OB = $\sqrt{5}$ > R
Do đó B nằm ngoài đường tròn (O ; 2)
$OC^2$ = $x^2_C$ + $y^2_C$ = $(\sqrt{2})^2$ + $(\sqrt{2})^2$ = 4
=> OC = $\sqrt{4}$ = 2 = R
Do đó C nằm trên đường tròn (O ; 2)
Giải bài 5 trang 100 sgk hình học 9 tập 1
Đố. Một tấm bìa hình tròn không còn dấu vết của tâm. Hãy tìm lại tâm của hình tròn đó.Bài giải:
 |
| Tâm hình tròn ở đâu? |
- Tương tự như vậy, gấp tấm bìa theo một nếp gấp khác, ta được đường kính thứ hai.
Giao điểm của hai đường kính đó chính là tâm của đường tròn.
Hoặc có thể làm theo cách:
- Lấy ba điểm A, B, C phân biệt trên đường tròn
- Nối A với B, A với C
- Dựng đường trung trực của AB, AC.
Hai đường trung trực này cắt nhau tại O. Đó chính là tâm của đường tròn.
Xem bài trước: Sự xác định đường tròn. Tính chất đối xứng của đường tròn.
EmoticonEmoticon