Giải bài tập cung chứa góc.
Lý thuyết về cung chứa góc mà cô giáo dạy trên lớp dường như rất rắc rối. Nhưng với những gì cô giáo cung cấp, tuy hơi khó hiểu, nhưng với một chút cần cù, giải bài tập cung chứa góc sẽ bù cho những rắc rối đó.
Bài giải:
Ta có:
$\widehat{I_1}$ = $\widehat{A_1}$ + $\widehat{B_1}$ (1) ($\widehat{I_1}$ là góc ngoài của tam giác ABI)
$\widehat{I_2}$ = $\widehat{A_2}$ + $\widehat{C_1}$ (2) ($\widehat{I_2}$ là góc ngoài của tam giác ACI)
Cộng (1) với (2) vế theo vế, ta được:
$\widehat{I_1}$ + $\widehat{I_2}$ = $\widehat{A_1}$ + $\widehat{A_2}$ + $\widehat{B_1}$ + $\widehat{C_1}$ (3)
Theo giả thiết $\widehat{A}$ = $90^0$ nên $\widehat{B}$ + $\widehat{C}$ = $90^0$ (định lí tổng ba góc của một tam giác)
Do đó $\widehat{A_1}$ + $\widehat{A_2}$ = $90^0$ (4)
Cũng theo giả thiết ta có:
$\widehat{B_1}$ = $\frac{\widehat{B}}{2}$ (BI là phân giác góc B)
$\widehat{C_1}$ = $\frac{\widehat{C}}{2}$ (CI là phân giác góc C)
Nên $\widehat{B_1}$ + $\widehat{C_1}$ = $\frac{\widehat{B} + \widehat{C}}{2}$ = $\frac{90}{2}$ = $45^0$ (5)
Thay (4) và (5) vào (3), ta được:
$\widehat{I_1}$ + $\widehat{I_2}$ = $90^0$ + $45^0$ = $135^0$
Hay $\widehat{BIC}$ = $135^0$
Như vậy, điểm I nhìn đoạn BC cố định dưới một góc $135^0$ không đổi. Do đó, quỹ tích của điểm I là cung chứa góc $135^0$ dựng trên đoạn thẳng BC.
Giải bài 44 trang 86 sgk hình học 9 tập 2.
Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường phân giác trong. Tìm quỹ tích điểm I khi A thay đổi.Bài giải:
 |
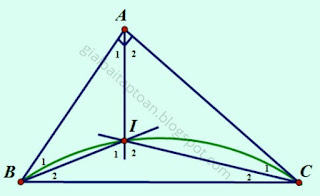| Quỹ tích điểm I khi A thay đổi. |
$\widehat{I_1}$ = $\widehat{A_1}$ + $\widehat{B_1}$ (1) ($\widehat{I_1}$ là góc ngoài của tam giác ABI)
$\widehat{I_2}$ = $\widehat{A_2}$ + $\widehat{C_1}$ (2) ($\widehat{I_2}$ là góc ngoài của tam giác ACI)
Cộng (1) với (2) vế theo vế, ta được:
$\widehat{I_1}$ + $\widehat{I_2}$ = $\widehat{A_1}$ + $\widehat{A_2}$ + $\widehat{B_1}$ + $\widehat{C_1}$ (3)
Theo giả thiết $\widehat{A}$ = $90^0$ nên $\widehat{B}$ + $\widehat{C}$ = $90^0$ (định lí tổng ba góc của một tam giác)
Do đó $\widehat{A_1}$ + $\widehat{A_2}$ = $90^0$ (4)
Cũng theo giả thiết ta có:
$\widehat{B_1}$ = $\frac{\widehat{B}}{2}$ (BI là phân giác góc B)
$\widehat{C_1}$ = $\frac{\widehat{C}}{2}$ (CI là phân giác góc C)
Nên $\widehat{B_1}$ + $\widehat{C_1}$ = $\frac{\widehat{B} + \widehat{C}}{2}$ = $\frac{90}{2}$ = $45^0$ (5)
Thay (4) và (5) vào (3), ta được:
$\widehat{I_1}$ + $\widehat{I_2}$ = $90^0$ + $45^0$ = $135^0$
Hay $\widehat{BIC}$ = $135^0$
Như vậy, điểm I nhìn đoạn BC cố định dưới một góc $135^0$ không đổi. Do đó, quỹ tích của điểm I là cung chứa góc $135^0$ dựng trên đoạn thẳng BC.
Giải bài 45 trang 86 sgk hình học 9 tập 2.
Cho các hình thoi ABCD có cạnh AB cố định. Tìm quỹ tích giao điểm O của hai đường chéo trong các hình thoi đó.
Bài giải:
Theo giả thiết ABCD là hình thoi nên:
AC $\perp$ BD (hai đường chéo vuông góc)
Hay $\widehat{AOB}$ = $90^0$
Như vậy, điểm O nhìn đoạn AB cố định dưới một góc $90^0$. Do đó quỹ tích điểm O là nửa đường tròn đường kính AB.
 |
| Quỹ tích giao điểm hai đường chéo hình thoi. |
AC $\perp$ BD (hai đường chéo vuông góc)
Hay $\widehat{AOB}$ = $90^0$
Như vậy, điểm O nhìn đoạn AB cố định dưới một góc $90^0$. Do đó quỹ tích điểm O là nửa đường tròn đường kính AB.
Giải bài 46 trang 86 sgk hình học 9 tập 2.
Dựng một cung chứa góc $55^0$ trên đoạn thẳng AB = 3cm.
Bài giải:
Với yêu cầu của đề bài, ta bắt đầu dựng như sau:
- Trước hết, dùng thước đo độ dài, dựng đoạn AB = 3cm
- Tiếp theo, dùng thước đo góc, dựng $\widehat{xAB}$ = $55^0$
- Tiếp tục, dùng ê ke dựng tia Ay vuông góc với Ax.
- Sau đó, dựng đường trung trực (d) của đoạn thẳng AB. Gọi O là giao điểm của Ay và (d)
- Cuối cùng, dựng đường tròn tâm O bán kính OA.
Ta được cung AmB là cung chứa góc $55^0$ dựng trên đoạn AB = 3cm.
Bài giải:
 |
| Dựng cung chứa góc 55 độ |
- Trước hết, dùng thước đo độ dài, dựng đoạn AB = 3cm
- Tiếp theo, dùng thước đo góc, dựng $\widehat{xAB}$ = $55^0$
- Tiếp tục, dùng ê ke dựng tia Ay vuông góc với Ax.
- Sau đó, dựng đường trung trực (d) của đoạn thẳng AB. Gọi O là giao điểm của Ay và (d)
- Cuối cùng, dựng đường tròn tâm O bán kính OA.
Ta được cung AmB là cung chứa góc $55^0$ dựng trên đoạn AB = 3cm.
Giải bài 47 trang 86 sgk hình học 9 tập 2.
Gọi cung chứa góc $55^0$ ở bài tập 46 là cung AmB. Lấy điểm $M_1$ nằm bên trong và điểm $M_2$ nằm bên ngoài đường tròn chứa cung này sao cho $M_1$, $M_2$ và cung AmB nằm cùng một phía đối với đường thẳng AB. Chứng minh rằng:
a) $\widehat{AM_1B}$ > $55^0$
b) $\widehat{AM_2B}$ < $55^0$
Bài giải:
a) Chứng minh $\widehat{AM_1B}$ > $55^0$
Gọi A', B' theo thứ tự là giao điểm của A$M_1$ và B$M_1$ với cung tròn AmB.
Theo đề $M_1$ là điểm bất kì nằm trong đường tròn chứa cung chứa góc $55^0$. Khi đó $\widehat{AM_1B}$ là góc có đỉnh ở bên trong đường tròn nên ta có:
$\widehat{AM_1B}$ = $\frac{1}{2}$(sđ⁀AB + sđ⁀A'B') = $\frac{sđ⁀AB }{2}$ + $\frac{sđ⁀A'B' }{2}$ = $55^0$ + $\frac{sđ⁀A'B' }{2}$
Vì $\frac{sđ⁀A'B' }{2}$ > 0
Nên $55^0$ + $\frac{sđ⁀A'B' }{2}$ > $55^0$
Vậy $\widehat{AM_1B}$ > $55^0$ (đpcm)
b) Chứng minh $\widehat{AM_2B}$ < $55^0$
Tương tự, ta gọi A', B' theo thứ tự là giao điểm của A$M_2$ và B$M_2$ với cung AmB.
Theo đề $M_2$ là điểm bất kì nằm ngoài đường tròn chứa cung chứa góc $55^0$. Khi đó $\widehat{AM_2B}$ là góc có đỉnh ở bên ngoài đường tròn nên:
$\widehat{AM_2B}$ = $\frac{1}{2}$(sđ⁀AB - sđ⁀A'B') = $\frac{sđ⁀AB }{2}$ - $\frac{sđ⁀A'B' }{2}$ = $55^0$ - $\frac{sđ⁀A'B' }{2}$
Vì $\frac{sđ⁀A'B' }{2}$ > 0 nên $55^0$ - $\frac{sđ⁀A'B' }{2}$ < $55^0$
Vậy $\widehat{AM_2B}$ < $55^0$ (đpcm)
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
a) Chứng minh $\widehat{AM_1B}$ > $55^0$
Theo đề $M_1$ là điểm bất kì nằm trong đường tròn chứa cung chứa góc $55^0$. Khi đó $\widehat{AM_1B}$ là góc có đỉnh ở bên trong đường tròn nên ta có:
$\widehat{AM_1B}$ = $\frac{1}{2}$(sđ⁀AB + sđ⁀A'B') = $\frac{sđ⁀AB }{2}$ + $\frac{sđ⁀A'B' }{2}$ = $55^0$ + $\frac{sđ⁀A'B' }{2}$
Vì $\frac{sđ⁀A'B' }{2}$ > 0
Nên $55^0$ + $\frac{sđ⁀A'B' }{2}$ > $55^0$
Vậy $\widehat{AM_1B}$ > $55^0$ (đpcm)
b) Chứng minh $\widehat{AM_2B}$ < $55^0$
Theo đề $M_2$ là điểm bất kì nằm ngoài đường tròn chứa cung chứa góc $55^0$. Khi đó $\widehat{AM_2B}$ là góc có đỉnh ở bên ngoài đường tròn nên:
$\widehat{AM_2B}$ = $\frac{1}{2}$(sđ⁀AB - sđ⁀A'B') = $\frac{sđ⁀AB }{2}$ - $\frac{sđ⁀A'B' }{2}$ = $55^0$ - $\frac{sđ⁀A'B' }{2}$
Vì $\frac{sđ⁀A'B' }{2}$ > 0 nên $55^0$ - $\frac{sđ⁀A'B' }{2}$ < $55^0$
Vậy $\widehat{AM_2B}$ < $55^0$ (đpcm)
EmoticonEmoticon