[Toán 7] Chứng minh BD là tia phân giác của góc B.
Ngày 23/2/2018 bạn Tiến Đạt gửi bài tập:
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua E vuông góc với BC cắt AC tại D.
a) Tính độ dài cạnh BC.
b) Chứng minh BD là tia phân giác của góc B.
c) Biết góc B bằng $60^0$, tam giác ABE là tam giác gì? Vì sao?
Trả lời cho bạn:
Xem lại những kiến thức đã học về định lí Py-ta-go, tam giác cân, trường hợp bằng nhau của hai tam giác vuông, bạn sẽ hoàn thành bài tập này một cách nhanh chóng.
a) Tính độ dài cạnh BC.
Áp dụng định lí Py-ta-go trong tam giác ABC vuông tại A, ta có:
$BC^2$ = $AB^2$ + $AC^2$ = $8^2$ + $6^2$ = 100
=> BC = $\sqrt{100}$ = 10
Vậy BC = 10 cm.
b) Xét hai tam giác vuông ADB và EDB có:
Cạnh BD chung
BA = BE (gt)
Vậy $\Delta$ ADB = $\Delta$ EDB (cạnh huyền - cạnh góc vuông)
Suy ra $\widehat{ABD}$ = $\widehat{EBD}$
Do đó BD là tia phân giác của góc ABE, hay BD là tia phân giác của góc B (đpcm)
c) Ta có BE = BA nên tam giác ABE cân tại B.
Mà $\widehat{B}$ = $60^0$
Do đó $\Delta$ ABE là tam giác đều.
➤ Trả lời cho bạn Kiều Linh
Cho tam giác ABC cân tại A ($\widehat{A}$ < $90^0$) có AB = AC = 10cm, BC = 16 cm. Kẻ AH vuông góc với BC.
a) Chứng minh rằng $\Delta$ ABH = $\Delta$ ACH
b) Tính độ dài AH
c) Kẻ HD $\perp$ AB, HE $\perp$ AC. Chứng minh rằng $\Delta$ BDH = $\Delta$ CEH
d) Nếu $\widehat{BAC}$ = $60^0$ thì $\Delta$ ADE là tam giác gì?
a) Chứng minh rằng $\Delta$ ABH = $\Delta$ ACH
Xét hai tam giác vuông HAB và HAC có:
Cạnh AH chung
AB = AC (gt)
Vậy $\Delta$ ABH = $\Delta$ ACH (cạnh huyền - cạnh góc vuông)
b) Tính AH
Ta có tam giác ABC cân tại A nên đường cao AH cũng là đường trung tuyến.
Do đó: BH = HC = $\frac{1}{2}$BC = $\frac{16}{2}$ = 8 cm
Áp dụng định lí Py-ta-go vào tam giác AHC vuông tại H, ta có:
$AC^2$ = $AH^2$ + $HC^2$
=> $AH^2$ = $AC^2$ - $HC^2$ = $10^2$ - $8^2$ = 100 - 64 = 36
=> AH = $\sqrt{36}$ = 6 cm.
c) Chứng minh rằng $\Delta$ BDH = $\Delta$ CEH
Xét hai tam giác vuông BDH và CEH có:
BH = CH (cmt)
$\widehat{DBH}$ = $\widehat{ECH}$ (vì tam giác ABC cân tại A)
Vậy $\Delta$ BDH = $\Delta$ CEH (cạnh huyền - góc nhọn)
d) Ta có $\Delta$ BDH = $\Delta$ CEH (cmt)
Suy ra BD = CE (hai cạnh tương ứng)
Mà AB = AC (gt)
Nên AD = AE
Suy ra tam giác ADE cân.
Nên nếu $\widehat{BAC}$ = $60^0$ thì $\Delta$ ADE là tam giác đều.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Cho tam giác ABC vuông tại A, AB = 8cm, AC = 6cm. Trên cạnh BC lấy điểm E sao cho BE = BA. Đường thẳng qua E vuông góc với BC cắt AC tại D.
a) Tính độ dài cạnh BC.
b) Chứng minh BD là tia phân giác của góc B.
c) Biết góc B bằng $60^0$, tam giác ABE là tam giác gì? Vì sao?
Trả lời cho bạn:
Xem lại những kiến thức đã học về định lí Py-ta-go, tam giác cân, trường hợp bằng nhau của hai tam giác vuông, bạn sẽ hoàn thành bài tập này một cách nhanh chóng.
a) Tính độ dài cạnh BC.
Áp dụng định lí Py-ta-go trong tam giác ABC vuông tại A, ta có:
$BC^2$ = $AB^2$ + $AC^2$ = $8^2$ + $6^2$ = 100
=> BC = $\sqrt{100}$ = 10
Vậy BC = 10 cm.
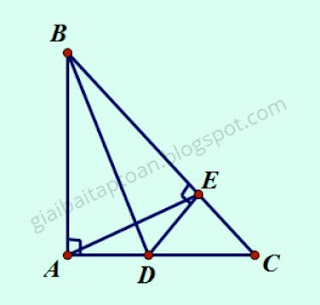 |
| Tam giác ABC vuông tại A. |
Cạnh BD chung
BA = BE (gt)
Vậy $\Delta$ ADB = $\Delta$ EDB (cạnh huyền - cạnh góc vuông)
Suy ra $\widehat{ABD}$ = $\widehat{EBD}$
Do đó BD là tia phân giác của góc ABE, hay BD là tia phân giác của góc B (đpcm)
c) Ta có BE = BA nên tam giác ABE cân tại B.
Mà $\widehat{B}$ = $60^0$
Do đó $\Delta$ ABE là tam giác đều.
➤ Trả lời cho bạn Kiều Linh
Cho tam giác ABC cân tại A ($\widehat{A}$ < $90^0$) có AB = AC = 10cm, BC = 16 cm. Kẻ AH vuông góc với BC.
a) Chứng minh rằng $\Delta$ ABH = $\Delta$ ACH
b) Tính độ dài AH
c) Kẻ HD $\perp$ AB, HE $\perp$ AC. Chứng minh rằng $\Delta$ BDH = $\Delta$ CEH
d) Nếu $\widehat{BAC}$ = $60^0$ thì $\Delta$ ADE là tam giác gì?
 |
| Tam giác ABC cân tại A. |
Xét hai tam giác vuông HAB và HAC có:
Cạnh AH chung
AB = AC (gt)
Vậy $\Delta$ ABH = $\Delta$ ACH (cạnh huyền - cạnh góc vuông)
b) Tính AH
Ta có tam giác ABC cân tại A nên đường cao AH cũng là đường trung tuyến.
Do đó: BH = HC = $\frac{1}{2}$BC = $\frac{16}{2}$ = 8 cm
Áp dụng định lí Py-ta-go vào tam giác AHC vuông tại H, ta có:
$AC^2$ = $AH^2$ + $HC^2$
=> $AH^2$ = $AC^2$ - $HC^2$ = $10^2$ - $8^2$ = 100 - 64 = 36
=> AH = $\sqrt{36}$ = 6 cm.
c) Chứng minh rằng $\Delta$ BDH = $\Delta$ CEH
Xét hai tam giác vuông BDH và CEH có:
BH = CH (cmt)
$\widehat{DBH}$ = $\widehat{ECH}$ (vì tam giác ABC cân tại A)
Vậy $\Delta$ BDH = $\Delta$ CEH (cạnh huyền - góc nhọn)
d) Ta có $\Delta$ BDH = $\Delta$ CEH (cmt)
Suy ra BD = CE (hai cạnh tương ứng)
Mà AB = AC (gt)
Nên AD = AE
Suy ra tam giác ADE cân.
Nên nếu $\widehat{BAC}$ = $60^0$ thì $\Delta$ ADE là tam giác đều.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon