Cung chứa góc.
Tính chất đường trung tuyến trong tam giác vuông, quỹ tích đường tròn, định lí góc nội tiếp, góc tạo bởi tia tiếp tuyến và dây cung ... là hành trang cần mang theo trong quá trình khám phá "cung chứa góc". Cung chứa góc dựng trên một đoạn thẳng là một thuật ngữ mới. Bài học hôm nay đòi hỏi phải tập trung cao độ mới có thể hiểu được. Ta sẽ bắt đầu với bài toán quỹ tích cung chứa góc.
Quỹ đạo chuyển động của điểm M có thể dự đoán qua các phần thực hành sau:
Cho đoạn thẳng CD. Vẽ ba điểm $N_1$, $N_2$, $N_3$ sao cho $\widehat{CN_1D}$ = $\widehat{CN_2D}$ = $\widehat{CN_3D}$ = $90^0$. Sau đó chứng minh rằng các điểm $N_1$, $N_2$, $N_3$ nằm trên đường tròn đường kính CD.
Ta sẽ chứng minh như sau:
Gọi O là trung điểm của CD
Theo tính chất tam giác vuông, $\Delta CN_1D$, $\Delta CN_2D$, $\Delta CN_3D$ là các tam giác vuông có chung cạnh huyền CD nên:
$N_1$O = $N_2$O = $N_3$O = $\frac{CD}{2}$
Suy ra $N_1$, $N_2$, $N_3$ cùng nằm trên đường tròn (O ; $\frac{CD}{2}$)
Tức ba điểm $N_1$, $N_2$, $N_3$ cùng nằm trên đường tròn đường kính CD.
Đó là trường hơp $\alpha$ = $90^0$. Một câu hỏi được đặt ra là nếu $\alpha$ $\neq$ $90^0$ thì sao? Tiếp tục thực hiện theo phần ?2 trong SGK, ta có dự đoán điểm M chuyển động trên hai cung tròn có hai đầu mút là A và B.
Đến đây ta sẽ chứng minh quỹ tích cần tìm là hai cung tròn.
a) Phần thuận:
Ta xét điểm M thuộc một nửa mặt phẳng có bờ là đường thẳng AB.
Giả sử M là điểm thỏa mãn $\widehat{AMB}$ = $\alpha$. Vẽ cung AmB đi qua ba điểm A, M, B. Ta sẽ xét xem tâm O của đường tròn chứa cung AmB có phụ thuộc vào vị trí của điểm M không?
Vẽ tiếp tuyến Ax của đường tròn chứa cung AmB, ta có:
$\widehat{BAx}$ = $\widehat{AMB}$ = $\alpha$ (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AnB)
Vì góc $\alpha$ cho trước nên tia Ax cố định.
Tâm O phải nằm trên tia Ay vuông góc với Ax tại A nên Ay cô định.
O cách đều hai điểm A và B nên O nằm trên đường trung trực d của AB.
Khi đó O là giao điểm của tia Ay cố định và đường trung trực d.
Suy ra O là một điểm cố định, không phụ thuộc vị trí của điểm M.
Theo giả thiết $0^0$ < $\alpha$ < $180^0$ nên Ay không thể vuông góc với AB và Ay lúc nào cũng cắt đường trung trực d của AB)
Vậy M thuộc cung tròn AmB cố định tâm O bán kính OA.
Lưu ý: Hình 40a ứng với góc $\alpha$ nhọn, hình 40b ứng với góc $\alpha$ tù.
b) Phần đảo:
Lấy điểm M' bất kỳ thuộc cung AmB, ta sẽ chứng minh $\widehat{AM'B}$ = $\alpha$
Ta có:
$\widehat{AM'B}$ là góc nội tiếp
$\widehat{xAB}$ là góc tạo bởi tia tiếp tuyến Ax và dây cung AB
Mà hai góc AM'B và xAB cùng chắn cung AnB
Nên $\widehat{xAB}$ = $\widehat{AM'B}$ = $\alpha$.
Tương tự trên nửa mặt phẳng đối của nửa mặt phẳng chứa điểm M đang xét còn có cung Am'B đối xứng với cung AmB qua AB cũng có tính chất như cung AmB.
Mỗi cung trên được gọi là một cung chứa góc $\alpha$ dựng trên đoạn thẳng AB, tức là cung mà với mọi điểm M thuộc cung đó, ta đều có $\widehat{AMB}$ = $\alpha$
c) Kết luận: Với đoạn thẳng AB và góc $\alpha$ ($0^0$ < $\alpha$ < $180^0$) cho trước thì quỹ tích các điểm M thỏa mãn $\widehat{AMB}$ = $\alpha$ là hai cung chứa góc $\alpha$ dựng trên đoạn AB.
➤ Chú ý:
- Hai cung chứa góc $\alpha$ nói trên là hai cung tròn đối xứng với nhau qua AB.
- Hai điểm A, B được coi là thuộc quỹ tích
- Khi $\alpha$ = $90^0$ thì hai cung AmB và Am'B là hai nửa đường tròn đường kính AB. Như vậy ta có: Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
- Trên hình 41, cung AmB là cung chứa góc $\alpha$ thì cung AnB là cung chứa góc $180^0$ - $\alpha$.
1) Dựng đường trung trực d của đoạn thẳng AB
2) Vẽ tia Ax sao cho $\widehat{BAx}$ = $\alpha$
3) Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d
4) Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.
5) Vẽ cung Am'B đối xứng với cung AmB qua AB
Phần thuận: Mọi điểm có tính chất T đều thuộc hình H
Phần đảo: Mọi điểm thuộc hình H đều có tính chât T.
Kết luận: Quỹ tích các điểm M có tính chất T là hình H.
Như vậy, trong bài toán quỹ tích cung chứa góc, tính chất T của các điểm M là tính chất nhìn đoạn thẳng AB cho trước dưới một góc bằng $\alpha$ (hay $\widehat{AMB}$ = $\alpha$ không đổi). Hình H trong bài toán này là hai cung chứa góc $\alpha$ dựng trên đoạn AB.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Bài toán quỹ tích "cung chứa góc"
Bài toán:
Cho đoạn thẳng AB và góc $\alpha$ ($0^0$ < $\alpha$ < $180^0$), Tìm quỹ tích các điểm M thỏa mãn $\widehat{AMB}$ = $\alpha$. Nói cách khác là tìm tập hợp các điểm M nhìn đoạn thẳng AB cho trước dưới một góc $\alpha$.Quỹ đạo chuyển động của điểm M có thể dự đoán qua các phần thực hành sau:
Cho đoạn thẳng CD. Vẽ ba điểm $N_1$, $N_2$, $N_3$ sao cho $\widehat{CN_1D}$ = $\widehat{CN_2D}$ = $\widehat{CN_3D}$ = $90^0$. Sau đó chứng minh rằng các điểm $N_1$, $N_2$, $N_3$ nằm trên đường tròn đường kính CD.
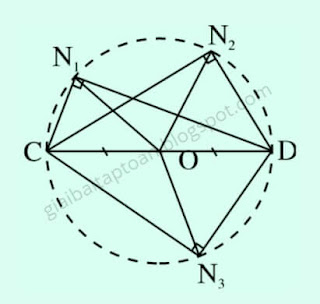 |
| O là trung điểm của CD. |
Ta sẽ chứng minh như sau:
Gọi O là trung điểm của CD
Theo tính chất tam giác vuông, $\Delta CN_1D$, $\Delta CN_2D$, $\Delta CN_3D$ là các tam giác vuông có chung cạnh huyền CD nên:
$N_1$O = $N_2$O = $N_3$O = $\frac{CD}{2}$
Suy ra $N_1$, $N_2$, $N_3$ cùng nằm trên đường tròn (O ; $\frac{CD}{2}$)
Tức ba điểm $N_1$, $N_2$, $N_3$ cùng nằm trên đường tròn đường kính CD.
Đó là trường hơp $\alpha$ = $90^0$. Một câu hỏi được đặt ra là nếu $\alpha$ $\neq$ $90^0$ thì sao? Tiếp tục thực hiện theo phần ?2 trong SGK, ta có dự đoán điểm M chuyển động trên hai cung tròn có hai đầu mút là A và B.
Đến đây ta sẽ chứng minh quỹ tích cần tìm là hai cung tròn.
a) Phần thuận:
Ta xét điểm M thuộc một nửa mặt phẳng có bờ là đường thẳng AB.
Giả sử M là điểm thỏa mãn $\widehat{AMB}$ = $\alpha$. Vẽ cung AmB đi qua ba điểm A, M, B. Ta sẽ xét xem tâm O của đường tròn chứa cung AmB có phụ thuộc vào vị trí của điểm M không?
 |
| Hình 40a |
$\widehat{BAx}$ = $\widehat{AMB}$ = $\alpha$ (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung AnB)
Vì góc $\alpha$ cho trước nên tia Ax cố định.
Tâm O phải nằm trên tia Ay vuông góc với Ax tại A nên Ay cô định.
O cách đều hai điểm A và B nên O nằm trên đường trung trực d của AB.
Khi đó O là giao điểm của tia Ay cố định và đường trung trực d.
Suy ra O là một điểm cố định, không phụ thuộc vị trí của điểm M.
Theo giả thiết $0^0$ < $\alpha$ < $180^0$ nên Ay không thể vuông góc với AB và Ay lúc nào cũng cắt đường trung trực d của AB)
Vậy M thuộc cung tròn AmB cố định tâm O bán kính OA.
Lưu ý: Hình 40a ứng với góc $\alpha$ nhọn, hình 40b ứng với góc $\alpha$ tù.
b) Phần đảo:
Lấy điểm M' bất kỳ thuộc cung AmB, ta sẽ chứng minh $\widehat{AM'B}$ = $\alpha$
Ta có:
$\widehat{AM'B}$ là góc nội tiếp
$\widehat{xAB}$ là góc tạo bởi tia tiếp tuyến Ax và dây cung AB
Mà hai góc AM'B và xAB cùng chắn cung AnB
Nên $\widehat{xAB}$ = $\widehat{AM'B}$ = $\alpha$.
 |
| Hình 41 |
Mỗi cung trên được gọi là một cung chứa góc $\alpha$ dựng trên đoạn thẳng AB, tức là cung mà với mọi điểm M thuộc cung đó, ta đều có $\widehat{AMB}$ = $\alpha$
c) Kết luận: Với đoạn thẳng AB và góc $\alpha$ ($0^0$ < $\alpha$ < $180^0$) cho trước thì quỹ tích các điểm M thỏa mãn $\widehat{AMB}$ = $\alpha$ là hai cung chứa góc $\alpha$ dựng trên đoạn AB.
➤ Chú ý:
- Hai cung chứa góc $\alpha$ nói trên là hai cung tròn đối xứng với nhau qua AB.
- Hai điểm A, B được coi là thuộc quỹ tích
- Khi $\alpha$ = $90^0$ thì hai cung AmB và Am'B là hai nửa đường tròn đường kính AB. Như vậy ta có: Quỹ tích các điểm nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB.
- Trên hình 41, cung AmB là cung chứa góc $\alpha$ thì cung AnB là cung chứa góc $180^0$ - $\alpha$.
Cách vẽ cung chứa góc $\alpha$
Qua cách chứng minh phần thuận, ta có thể khái quát cách vẽ một cung chứa góc $\alpha$ trên đoạn AB như sau:1) Dựng đường trung trực d của đoạn thẳng AB
2) Vẽ tia Ax sao cho $\widehat{BAx}$ = $\alpha$
3) Vẽ đường thẳng Ay vuông góc với Ax. Gọi O là giao điểm của Ay với d
4) Vẽ cung AmB, tâm O, bán kính OA sao cho cung này nằm ở nửa mặt phẳng bờ AB không chứa tia Ax.
5) Vẽ cung Am'B đối xứng với cung AmB qua AB
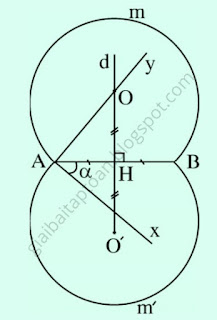 |
| Cách vẽ cung chứa góc $\alpha$ |
Cách giải bài toán quỹ tích
Qua bài toán trên, muốn chứng minh quỹ tích các điểm M thỏa mãn tính chất T là một hình H nào đó, ta phải chưng minh hai phần như sau:Phần thuận: Mọi điểm có tính chất T đều thuộc hình H
Phần đảo: Mọi điểm thuộc hình H đều có tính chât T.
Kết luận: Quỹ tích các điểm M có tính chất T là hình H.
Như vậy, trong bài toán quỹ tích cung chứa góc, tính chất T của các điểm M là tính chất nhìn đoạn thẳng AB cho trước dưới một góc bằng $\alpha$ (hay $\widehat{AMB}$ = $\alpha$ không đổi). Hình H trong bài toán này là hai cung chứa góc $\alpha$ dựng trên đoạn AB.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon