Giải SBT vị trí tương đối của đường thẳng và đường tròn.
Giải bài 35 trang 162 SBT toán 9 tập 1.
Trên mặt phẳng tọa độ cho điểm I có tọa độ (-3 ; 2). Nếu vẽ đường tròn tâm I bán kính bằng 2 thì đường tròn đó có vị trí tương đối như thế nào đối với các trục tọa độ.Bài giải:
Theo đề ta có hình vẽ như sau:
 |
| Vị trí tương đối của điểm I đến trục tọa độ. |
Kẻ IB $\perp$ Oy. Khi đó IB = 3 > R nên đường tròn (I) và trục tung không giao nhau.
Giải bài 37 trang 162 SBT toán 9 tập 1.
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm)
a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy.
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
Bài giải:
a) Kẻ AK $\perp$ xy.
Ta có AK < AC ( cạnh huyền lớn hơn cạnh góc vuông)
Nghĩa là d < R.
Nên đường tròn (A) và đường thẳng xy cắt nhau.
Suy ra đường tròn (A) có hai giao điểm với đường thẳng xy (đpcm)
b) Ta có AK = 12 cm, AC = 13 cm.
Áp dụng định lí Py-ta-go trong tam giác vuông AKC ta có:
$AC^2$ = $AK^2$ + $KC^2$
=> $KC^2$ = $AC^2$ - $AK^2$ = $13^2$ - $12^2$ = 169 - 144 = 25
=> KC = 5 cm.
Tam giác ABC cân tại A có AK là đường cao nên vừa là trung tuyến.
Suy ra BC = 2KC (K là trung điểm của BC)
<=> BC = 2.5 = 10
Vậy BC = 10 cm.
a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy.
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC.
Bài giải:
a) Kẻ AK $\perp$ xy.
 |
| Điểm A cách đường thẳng xy 12 cm. |
Nghĩa là d < R.
Nên đường tròn (A) và đường thẳng xy cắt nhau.
Suy ra đường tròn (A) có hai giao điểm với đường thẳng xy (đpcm)
b) Ta có AK = 12 cm, AC = 13 cm.
Áp dụng định lí Py-ta-go trong tam giác vuông AKC ta có:
$AC^2$ = $AK^2$ + $KC^2$
=> $KC^2$ = $AC^2$ - $AK^2$ = $13^2$ - $12^2$ = 169 - 144 = 25
=> KC = 5 cm.
Tam giác ABC cân tại A có AK là đường cao nên vừa là trung tuyến.
Suy ra BC = 2KC (K là trung điểm của BC)
<=> BC = 2.5 = 10
Vậy BC = 10 cm.
Giải bài 39 trang 162 SBT toán 9 tập 1.
Cho hình thang vuông ABCD ($\widehat{A}$ = $\widehat{D}$ = $90^0$), AB = 4cm, BC = 13cm, CD = 9cm.a) Tính độ dài AD
b) Chứng minh rằng đường thẳng AD tiếp xúc với đường tròn có đường kính là BC
Bài giải:
a) Kẻ BH $\perp$ CD. Khi đó ABHD là hình chữ nhật.
Nên DH = AB = 4cm, AD = BH
Suy ra HC = 5cm (HC = CD - DH)
Áp dụng định lí Py-ta-go trong tam giác vuông BHC, ta có:
$BH^2$ + $HC^2$ = $BC^2$ => $BH^2$ = $BC^2$ - $HC^2$ = $13^2$ - $5^2$ = 169 - 25 = 144
=> BH = $\sqrt{144}$ = 12
Vậy AD = 12 cm.
 |
| Hình thang vuông ABCD. |
Bán kính của đường tròn (E) là
R = $\frac{BC}{2}$ = $\frac{13}{2}$ = 6,5 cm. (1)
Kẻ EK $\perp$ AD. Khi đó EK là đường trung bình của hình thang ABCD nên:
EK = $\frac{AB + CD}{2}$ = $\frac{4 + 9}{2}$ = 6,5 cm. (2)
Mà EK chính là khoảng cách d từ tâm E đến AD. (3)
Từ (1) (2) (3) suy ra d = R. Do đó đường tròn (E) tiếp xúc với AD. (đpcm)
Giải bài 40 trang 162 SBT toán 9 tập 1.
Cho đường tròn (O), bán kính OA, dây CD là đường trung trực của OA.a) Tứ giác OCAD là hình gì? Vì sao?
b) Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Tính độ dài CI biết OA = R.
Bài giải:
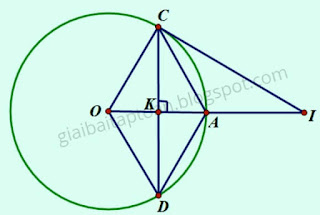 |
| CD là đường trung trực của OA. |
a) Gọi K là giao điểm của CD và OA.
Vì CD là đường trung trực của OA nên ta có:
OK = KA (1)
OA $\perp$ CD do đó CK = KD (2) (đường kính vuông góc với dây thì đi qua trung điểm của dây ấy)
Từ (1) và (2) suy ra tứ giác OCAD là hình bình hành.
Hình bình hành OCAD có hai đường chéo OA và CD vuông góc nên OCAD là hình thoi.
b) Ta có OA = OC (bán kính)
OA = CA (OCAD là hình thoi)
Nên tam giác AOC đều.
Suy ra $\widehat{AOC}$ = $60^0$
Ta có tam giác OCI vuông tại C (CI là tiếp tuyến đường tròn O)
Áp dụng tỉ số lượng giác của góc nhọn vào tam giác OCI ta có:
tg $\widehat{AOC}$ = $\frac{CI}{OC}$
<=> tg $60^0$ = $\frac{CI}{OC}$
<=> CI = OC.tg $60^0$ <=> CI = R.$\sqrt{3}$
Giải bài 41 trang 162 SBT toán 9 tập 1.
Cho nửa đường tròn tâm O, đường kính AB. Qua điểm C thuộc nửa đường tròn, kẻ tiếp tuyến d của đường tròn. Gọi E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d. Gọi H là chân đường vuông góc kẻ từ C đến AB. Chứng minh rằng:a) CE = CF
b) AC là tia phân giác của góc BAE.
c) $CH^2$ = AE. BF
Bài giải:
a) Ta có E và F lần lượt là chân các đường vuông góc kẻ từ A và B đến d nên
AE $\perp$ EF (1)
BF $\perp$ EF (2)
Từ (1) và (2) suy ra AE // BF. Do đó AEFB là hình thang.
Ta cũng có d (hay EF) là tiếp tuyến của (O) và C là tiếp điểm nên
OC $\perp$ EF (3)
Từ (1) (2) (3) suy ra OC // AE // BF
Mặt khác ta có OA = OB (= bán kính đường tròn O)
Điều đó cho thấy OC đi qua trung điểm O của cạnh bên AB và song song với hai đáy nên sẽ đi qua trung điểm của cạnh bên EF (theo định lí 3 về đường trung bình của hình thang)
Suy ra CE = CF (đpcm)
 |
| d la tiếp tuyến của đường tròn O |
b) Ta có OA = OC (= bán kính)
Nên tam giác OAC cân tại O.
Suy ra $\widehat{CAO}$ = $\widehat{ACO}$ (1)
Ta cũng có AE // OC (cmt)
Nên $\widehat{CAE}$ = $\widehat{ACO}$ (2) (hai góc so le trong)
Từ (1) và (2) suy ra $\widehat{CAO}$ = $\widehat{CAE}$
Do đó AC là tia phân giác của $\widehat{BAE}$
c) Xét hai tam giác vuông CAE và CAH có:
Cạnh AC chung
$\widehat{CAE}$ = $\widehat{ACO}$ (cmt)
Nên $\Delta$ CAE = $\Delta$ CAH (cạnh huyền - góc nhọn)
Suy ra AE = AH
Chứng minh tương tự ta được BF = BH
Ta có tam giác ABC nội tiếp đường tròn đường kính AB nên tam giác ABC vuông tại C.
Áp dụng hệ thức lượng liên quan tới đường cao trong tam giác vuông ABC, ta có:
$CH^2$ = HA.HB
Hay $CH^2$ = AE.BF (đpcm)
Xem lại vị trí tương đối của đường thẳng và đường tròn.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon