Đối xứng tâm.

Ở bài đối xứng trục, ta đã có những hiểu biết về hai điểm, hai hình đối xứng qua một đường thẳng. Liệu qua một điểm có thể có hai điểm hoặc hai hình nào đó đối xứng với nhau không. Để có câu trả lời ta cùng tìm hiểu bài đối xứng tâm.

Hai điểm đối xứng qua một điểm

Cho hai điểm A và O, các bạn dễ dàng vẽ được điểm A' sao cho O là trung điểm của đoạn thẳng AA' (hình 1)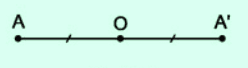

Hình 1. Điểm A' đối xứng với A qua O.

Khi đó A' là điểm đối xứng với điểm A qua điểm O và A là điểm đối xứng với điểm A' qua điểm O. Nói cách khác A và A' là hai điểm đối xứng nhau qua điểm O.
Ta đi đến định nghĩa hai điểm đối xứng qua một điểm như sau:

Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.

Có thể nhiều bạn sẽ thắc mắc khi đó điểm đối xứng với điểm O là điểm nào. Chưa thể đưa ra câu trả lời cho câu hỏi đó. Nhưng nếu câu hỏi là điểm đối xứng với điểm O qua điểm O là điểm nào sẽ có câu trả lời. Các bạn chỉ cần nhớ quy ước sau:

Điểm đối xứng với điểm O qua điểm O cũng là điểm O

Nếu thay điểm A, A' đó bằng những hình ảnh thì sao. Vấn đề này ta sẽ tìm hiểu ngay sau đây.

Hai hình đối xứng qua một điểm

Cho điểm O và đoạn thẳng AB.
Với khái niệm hai điểm đối xứng qua một điểm vừa tìm hiểu ở trên, ta dễ dàng vẽ được:
- điểm A' đối xứng với A qua O
- điểm B' đối xứng với B qua O
Theo các bạn ta sẽ vẽ điểm A' và B' như thế nào. Dĩ nhiên, các bạn cho rằng việc đó quá dễ dàng và thường cho qua. Hãy cứ vẽ thử đi vì rất có thể ngày mai cô giáo sẽ gọi ta lên bảng vẽ.
Xem như điểm A' và B' đã vẽ xong. Giờ lấy điểm C thuộc đoạn AB, vẽ điểm C' đối xứng với điểm C qua O. Các bạn không phải lo vì điểm C này cô giáo sẽ vẽ (ta thấy cô giáo thật...dễ thương). Nhưng lập tức cô lại đưa ra câu hỏi vị trí của điểm C có gì đặc biệt, làm bạn thật sự lúng túng. Tuy nhiên, bạn bất ngờ reo lên điểm C thuộc đoạn thẳng AB. (bạn thật là thông minh).

Hình 2. Đoạn A'B' đối xứng với đoạn AB qua điểm O

Vậy là đã vẽ xong hình theo đúng yêu cầu, ta đặt tên là hình 2. Nhìn vào hình 2, ta thấy mỗi điểm thuộc đoạn thẳng AB đối xứng với một điểm thuộc đoạn thẳng A'B' qua điểm O. Ta nói đoạn thẳng AB đối xứng với đoạn thẳng A'B' qua điểm O. Ta đi đến định nghĩa hai hình đối xứng qua một điểm như sau:

Hai hình gọi là đối xứng nhau qua điểm O nếu mỗi điểm thuộc hình này đối xứng với một điểm của hình kia qua điểm O và ngược lại.

Khi đó điểm O gọi là tâm đối xứng của hai hình.

Hình 3

Quan sát hình 3, ta thấy:
- Hai đoạn thẳng AB và A'B' đối xứng nhau qua tâm O
- Hai đường thẳng AC và A'C' đối xứng nhau qua tâm O
- Hai góc ABC và A'B'C' đối xứng nhau qua tâm O
- Hai tam giác ABC và A'B'C' đối xứng nhau qua tâm O
Qua đó ta cũng nhận thấy đoạn thẳng AB bằng A'B, góc ABC bằng góc A'B'C', tam giác ABC bằng tam giác A'B'C'. Điều đó cũng đã được chứng minh và cho ta tính chất sau:

Nếu hai đoạn thẳng (góc, tam giác) đối xứng nhau qua một điểm thì chúng bằng nhau

Hình H đối xứng với hình H' qua O.

Lúc này, cô giáo treo bức vẽ trên lên bảng, ta nhận ra ngay hình H và H' trong bức tranh đối xứng với nhau qua tâm O. Có bạn nào đó tinh nghịch hỏi nếu quay hình H quanh điểm O một góc $180^0$ thì chuyện gì sẽ xảy ra. Cô giáo ôn tồn bảo không có chuyện gì nghiêm trọng xảy ra đâu, hai hình chỉ trùng khít lên nhau thôi và nhấn mạnh điều đó một lần nữa chứng minh cho tính chất vừa đề cập ở trên.
Những tưởng bài học đến đây đã kết thúc, nhưng cô lại nêu tiếp một vấn đề trong thực tế, ta thường gặp những hình nào có tâm đối xứng. Vậy là phải tìm hiểu thêm hình có tâm đối xứng.

Hình có tâm đối xứng

Nối điểm A với B' và điểm B với A' trên hình 2, ta được hình bình hành ABA'B'. Khi đó ta có O là giao điểm của hai đường chéo và cũng là tâm đối xứng của hình bình hành ABA'B'.
Từ những phân tích ở mục hai hình đối xứng qua một điểm, ta có định nghĩa:

Điểm O gọi là tâm đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H. Nói cách khác hình H có tâm đối xứng.

Như vậy, hình bình hành là một hình có tâm đối xứng. Liên quan đến tâm đối xứng của hình bình hành có một định lí mà ta cần ghi nhớ đó là:

Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.

Tóm lại, bài viết thì dài dòng, các bạn chỉ cần hiểu được định nghĩa hai điểm đối xứng qua một điểm, hai hình đối xứng qua một điểm, khi nào thì một hình có tâm đối xứng, liên hệ với thực tế, áp dụng giải bài tập. Bên cạnh đó cũng cần có một chút kĩ năng về vẽ một điểm (hoặc một hình) đối xứng với một điểm (hoặc một hình) cho trước.

 Xem bài trước: Giải bài luyện tập hình bình hành

Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

CÙNG CHIA SẺ ĐỂ KIẾN THỨC ĐƯỢC LAN TỎA!

Be a Fan

Bài học liên quan.