Giải bài luyện tập 2 định lí Py-ta-go.
Giải bài 59 trang 133 sgk hình học 7 tập 1.
Bạn Tâm muốn đóng một nẹp chéo AC để chiếc khung hình chữ nhật ABCD được vững hơn (h.134). Tính độ dài AC, biết rằng AD = 48cm, CD = 36cm.Bài giải:
Hai cạnh AD và CD tạo với nẹp chéo AC tam giác ACD vuông tại D.
Áp dụng định lí Py-ta-go trong tam giác vuông ACD, ta có:
$AC^2$ = $AD^2$ + $CD^2$ = $48^2$ + $36^2$ = 2304 + 1296 = 3600.
=> AC = $\sqrt{3600}$ = 60
Vậy AC = 60 cm.
Giải bài 60 trang 133 sgk hình học 7 tập 1.
Cho tam giác nhọn ABC. Kẻ AH vuông góc với BC (H $\in$ BC). Cho biết AB = 13cm, AH = 12cm, HC = 16cm. Tính các độ dài AC, BC.Bài giải:
Áp dụng định lí Py-ta-go trong tam giác vuông HAC, ta có:
$AC^2$ = $HA^2$ + $HC^2$ = $12^2$ + $16^2$ = 144 + 256 = 400
=> AC = 20 cm.
Áp dụng định lí Py-ta-go trong tam giác vuông HAB, ta có:
$AB^2$ = $HA^2$ + $HB^2$
=> $HB^2$ = $AB^2$ - $HA^2$ = $13^2$ - $12^2$ = 169 - 144 = 25
=> HB = 5 cm.
Ta có BC = BH + HC (vì H $\in$ BC)
<=> BC = 5 + 16 = 21 cm
Vậy AC = 20 cm, BC = 21 cm.
Giải bài 61 trang 133 sgk hình học 7 tập 1.
Trên giấy kẻ ô vuông (độ dài của ô vuông bằng 1), cho tam giác ABC như hình 135. Tính độ dài mỗi cạnh của tam giác ABC.Bài giải:
Lấy ba điểm E, H, K ở vị trí như hình vẽ.
Áp dụng định lí Py-ta-go trong tam giác vuông ABH, ta có:
$AB^2$ = $HA^2$ + $HB^2$ = $2^2$ + $1^2$ = 5
=> AB = $\sqrt{5}$
Áp dụng định lí Py-ta-go trong tam giác vuông CEB, ta có:
$BC^2$ = $EC^2$ + $EB^2$ = $5^2$ + $3^2$ = 25 + 9 = 34
=> BC = $\sqrt{34}$
Áp dụng định lí Py-ta-go trong tam giác vuông KCA, ta có:
$AC^2$ = $CK^2$ + $AK^2$ = $4^2$ + $3^2$ = 16 + 9 = 25
=> AC = $\sqrt{25}$ = 5.
Vậy AB = $\sqrt{5}$ cm, BC = $\sqrt{34}$ cm, AC = 5 cm.
Giải bài 62 trang 133 sgk hình học 7 tập 1.
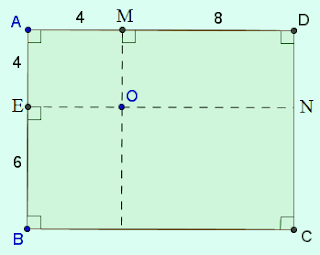
Đố: Người ta buộc con Cún bằng sợi dây có một đầu buộc tại điểm O làm cho con Cún cách điểm O nhiều nhất là 9m (h.136). Con Cún có thể tới các vị trí A, B, C, D để canh giữ mảnh vườn hình chữ nhật ABCD hay không? (Các kích thước như trên hình vẽ)Bài giải:
Muốn biết Cún con có thể đến được các vị trí A, B, C, D để canh giữ mảnh vườn hay không, ta tính các đoạn OA, OB, OC, OD.
Lấy các điểm E, M, N ở các vị trí như hình vẽ.
Áp dụng định lí Py-ta-go trong tam giác vuông OMA, ta có:
$OA^2$ = $OM^2$ + $MA^2$ = $3^2$ + $4^2$ = 9 + 16 = 25
=> OA = $\sqrt{25}$ = 5
Ta có OA = 5 m nhỏ hơn 9 m nên Cún con đến được điểm A.
Áp dụng định lí Py-ta-go trong tam giác vuông OEB, ta có:
$OB^2$ = $OE^2$ + $EB^2$ = $4^2$ + $6^2$ = 16 + 36 = 52
=> OB = $\sqrt{52}$ $\approx$ 7,2
Ta có OB = 7,2 m nhỏ hơn 9 m nên Cún con đến được điểm B.
Áp dụng định lí Py-ta-go trong tam giác vuông ONC, ta có:
$OC^2$ = $ON^2$ + $NC^2$ = $8^2$ + $6^2$ = 64 + 36 = 100
=> OC = $\sqrt{100}$ = 10.
Ta có OC = 10 m lớn hơn 9 m nên Cún con không đến được điểm C.
Áp dụng định lí Py-ta-go trong tam giác vuông OMD, ta có:
$OD^2$ = $OM^2$ + $MD^2$ = $3^2$ + $8^2$ = 9 + 64 = 73
=> OD = $\sqrt{73}$ $\approx$ 8,5
Ta có OD = 8,5 m nhỏ hơn 9 m nên Cún con đến được điểm D.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!



EmoticonEmoticon