Luyện tập bổ sung các khái niệm về hàm số.
Giải bài tập 4 trang 45 SGK đại số 9
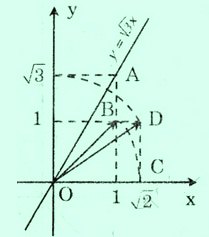
Đồ thị hàm số y = $\sqrt{3}$ x được vẽ bằng compa và thước thẳng như hình sau:
Hãy tìm hiểu và trình bày lại các bước thực hiện vẽ đồ thị đó.
Bài giải:
Ta biết rằng đồ thị hàm số y = $\sqrt{3}$ x là một đường thẳng đi qua gốc tọa độ.
Mặt khác, khi x = 1 thì y = $\sqrt{3}$. Do đó điểm A(1; $\sqrt{3}$) thuộc đồ thị. Vì thế để vẽ đồ thị này, ta phải xác định điểm A trên mặt phẳng tọa độ. Muốn vậy ta phải lấy một điểm biểu diễn số $\sqrt{3}$ trên trục tung. Ta có:
$\sqrt{3}$ = $\sqrt{2 + 1}$ = $\sqrt{(\sqrt{3})^2 + 1^2}$
Theo hình vẽ trên, ta có:
OB = $\sqrt{1 + 1}$ = $\sqrt{2}$ (áp dụng định lí Py-ta-go)
và OC = OB = $\sqrt{2}$
a) Vẽ đồ thị hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (h.5.SGK).và OC = OB = $\sqrt{2}$
Cũng theo hình vẽ trên và áp dụng định lý Py-ta-go, ta có:
OD = $\sqrt{OC^2 + CD^2}$ = $\sqrt{(\sqrt{3})^2 + 1^2}$ = $\sqrt{3}$
Đến đây, dùng compa ta xác định được điểm biểu diễn số $\sqrt{3}$ trên trục Oy. Từ đó xác định được điểm A.OD = $\sqrt{OC^2 + CD^2}$ = $\sqrt{(\sqrt{3})^2 + 1^2}$ = $\sqrt{3}$
Giải bài tập 5 trang 45 SGK đại số 9
b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ của các điểm A, B và tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimét.
Bài giải:
a) Đồ thị hàm số y = x và y = 2x được vẽ như sau:
 |
| Đồ thị hàm số y = x |
b) Tọa độ điểm A(2;4), điểm B(4;4)
Để tính chu vi tam giác OAB ta:
Dựng AH $\perp $ Ox. Ta có điểm H(2;0)
BI $\perp $ Ox. Ta có điểm I(4;0)
AK $\perp $ Oy. Ta có điểm K(0;4)
Ta có:
OH = $ \left | x_H \right | $ = 2
OI = $ \left | x_I \right | $ = 4
AH = BI = OK = $ \left | y_K \right | $ = 4
Ta lại có:
OA = $\sqrt{OH^2 + AH^2}$ = $\sqrt{4 + 16}$ = $\sqrt{20}$ = 2$\sqrt{5}$
OB = $\sqrt{OI^2 + BI^2}$ = $\sqrt{16 + 16}$ = $\sqrt{32}$ = 4$\sqrt{2}$
AB = HI = OI - OH = 4 - 2 = 2
Vậy:
Chu vi tam giác OAB = OA + OB + AB = 2$\sqrt{5}$ + 4$\sqrt{2}$ + 2
Diện tích tam giác OAB = $\frac{1}{2}$ . AB . OK = $\frac{1}{2}$ . 2 . 4 = 4
Giải bài tập 6 trang 45 SGK đại số 9
a) Tính giá trị y tương ứng với mỗi hàm số theo giá trị đã cho của biến x rồi điền vào bảng sau:
x
|
-2,5
|
-2,25
|
-1,5
|
-1
|
0
|
1
|
1,5
|
2,25
|
2,5
|
y = 0,5x
|
|||||||||
y = 0,5x + 2
|
Bài giải:
a) Với mỗi giá trị của x, ta có giá trị tương ứng của y như sau:
x
|
-2,5
|
-2,25
|
-1,5
|
-1
|
0
|
1
|
1,5
|
2,25
|
2,5
|
y = 0,5x
|
-1,25
|
-1,125
|
-0,75
|
-0,5
|
0
|
0,5
|
0,75
|
1,125
|
1,25
|
y = 0,5x + 2
|
0,75
|
0,875
|
1,25
|
1,5
|
2
|
2,5
|
2,75
|
3,125
|
3,25
|
Giải bài tập 7 trang 46 SGK đại số 9
Cho x hai giá trị bất kì $x_1$, $x_2$ sao cho $x_1$ < $x_2$
Hãy chứng minh f($x_1$ ) < f($x_2$ ) rồi rút ra kết luận hàm số đã cho đồng biến trên R.
Bài giải:
Ta có:
- Với giá trị $x_1$ thì hàm số nhận giá trị f($x_1$) = 3$x_1$
- Với giá trị $x_2$ thì hàm số nhận giá trị f($x_2$) = 3$x_2$
Xét hiệu f($x_1$) – f($x_2$) = 3$x_1$ – 3$x_2$
f($x_1$) – f($x_2$) = 3($x_1$ – $x_2$) (1)
Theo giả thiết $x_1$ < $x_2$ nên $x_1$ – $x_2$ < 0 (2)
Từ (1) và (2) ta suy ra: f($x_1$) – f($x_2$) < 0 <=> f($x_1$) < f($x_2$)
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
- Với giá trị $x_2$ thì hàm số nhận giá trị f($x_2$) = 3$x_2$
Xét hiệu f($x_1$) – f($x_2$) = 3$x_1$ – 3$x_2$
f($x_1$) – f($x_2$) = 3($x_1$ – $x_2$) (1)
Theo giả thiết $x_1$ < $x_2$ nên $x_1$ – $x_2$ < 0 (2)
Từ (1) và (2) ta suy ra: f($x_1$) – f($x_2$) < 0 <=> f($x_1$) < f($x_2$)
Vậy $x_1$ < $x_2$ => f($x_1$) < f($x_2$) (3)
Ta có (3) đúng với mọi giá trị bất kì của x ∈ R.
Mặt khác $x_1$, $x_2$ là hai số thực bất kì nên từ (3) ta kết luận hàm số y = 3x đồng biến trên tập số thực R.
Mặt khác $x_1$, $x_2$ là hai số thực bất kì nên từ (3) ta kết luận hàm số y = 3x đồng biến trên tập số thực R.

EmoticonEmoticon