Ôn tập chương I hình học 9 tập 1 (tt)
Giải bài 38 trang 95 sgk hình học 9 tập 1
Hai chiếc thuyền A và B ở vị trí được minh họa như hình 48. Tính khoảng cách giữa chúng (làm tròn đến mét)Bài giải:
 |
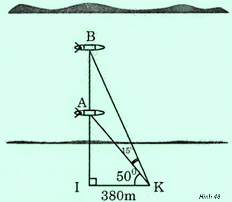| Hình 48 |
Áp dụng hệ thức về cạnh và góc trong tam giác vuông IKB, ta có:
IB = IK.tg $\widehat{IKB}$ = 380.tg($50^0$ + $15^0$) = 380.tg $65^0$ $\approx$ 380.2,14 = 814,9 (m)
Áp dụng hệ thức về cạnh và góc trong tam giác vuông IKA, ta có:
IA = IK.tg $\widehat{IKA}$ = 380.tg $50^0$ = 380.1,19 = 452,9 (m)
Vậy khoảng cách giữa hai thuyền là:
AB = IB - IA = 814,9 - 452,9 = 362 (m)
Giải bài 39 trang 95 sgk hình học 9 tập 1
Tìm khoảng cách giữa hai cọc để căng dây vượt qua vực trong hình 49 (làm tròn đến mét)
Bài giải:
Đặt tên các điểm như hình vẽ, ta có khoảng cách giữa hai cọc là BE
Ta có AC//DE => $\widehat{E}$ = $\widehat{C}$ = $50^0$
Áp dụng hệ thức về cạnh và góc trong tam giác vuông ABC, ta có:
AB = AC.tg $\widehat{C}$ = 20.tg$50^0$ = 20.1,19 = 23,83
Ta có BD = AB - AD = 23,83 - 5 = 18,83
Áp dụng tỉ số lượng giác vào tam giác vuông BDE, ta có:
sin $\widehat{E}$ = $\frac{BD}{BE}$ => BE = $\frac{BD}{sin 50^0}$ = $\frac{18,83}{sin 50^0}$ = 24,58 $\approx$ 25
Vậy khoảng cách giữa hai cọc là 25m
Áp dụng tỉ số lượng giác vào tam giác ABC, ta có:
tg $\widehat{ABC}$ = $\frac{AC}{BC}$ = $\frac{2}{5}$ = 0,4
<=> tg y = tg $21^0$48' <=> y = $21^0$48'
Khi đó x = $90^0$ - $21^0$48' = $68^0$12'
Vậy x - y = $68^0$12' - $21^0$48' = $46^0$34'
Bài giải:
 |
| Hình 49 |
Ta có AC//DE => $\widehat{E}$ = $\widehat{C}$ = $50^0$
Áp dụng hệ thức về cạnh và góc trong tam giác vuông ABC, ta có:
AB = AC.tg $\widehat{C}$ = 20.tg$50^0$ = 20.1,19 = 23,83
Ta có BD = AB - AD = 23,83 - 5 = 18,83
Áp dụng tỉ số lượng giác vào tam giác vuông BDE, ta có:
sin $\widehat{E}$ = $\frac{BD}{BE}$ => BE = $\frac{BD}{sin 50^0}$ = $\frac{18,83}{sin 50^0}$ = 24,58 $\approx$ 25
Vậy khoảng cách giữa hai cọc là 25m
Giải bài 40 trang 95 sgk hình học 9 tập 1
Tính chiều cao của cây trong hình 50 (làm tròn đến deximet)
Bài giải:
Chiều cao của cây là:
h = 30.tg $35^0$ + 1,7 $\approx$ 30.0,7 + 1,7 = 21 + 1,7 = 22,7 (m) = 227 (dm)
 |
| Hình 50 |
h = 30.tg $35^0$ + 1,7 $\approx$ 30.0,7 + 1,7 = 21 + 1,7 = 22,7 (m) = 227 (dm)
Giải bài 41 trang 96 sgk hình học 9 tập 1
Tam giác ABC vuông tại C có AC = 2cm, BC = 5cm, $\widehat{BAC}$ = x, $\widehat{ABC}$ = y. Dùng các thông tin sau (nếu cần) để tìm x - y:
sin $23^0$36' $\approx$ 0,4; cos $66^0$24' $\approx$ 0,4; tg $21^0$48' $\approx$ 0,4
Bài giải:Áp dụng tỉ số lượng giác vào tam giác ABC, ta có:
tg $\widehat{ABC}$ = $\frac{AC}{BC}$ = $\frac{2}{5}$ = 0,4
<=> tg y = tg $21^0$48' <=> y = $21^0$48'
Khi đó x = $90^0$ - $21^0$48' = $68^0$12'
Vậy x - y = $68^0$12' - $21^0$48' = $46^0$34'
Giải bài 42 trang 96 sgk hình học 9 tập 1
Ở một cái thang dài 3m người ta ghi: "Để đảm bảo an toàn khi dùng thang, phải đặt thang này tạo với mặt đất một góc có độ lớn từ $60^0$ đến $70^0$. Đo góc thì khó hơn đo độ dài. Vậy hãy cho biết: Khi dùng thang đó chân thang phải đặt cách tường khoảng bao nhiêu mét để đảm bảo an toàn?
Bài giải:
Chiều dài của cái thang là đoạn BC, khoảng cách từ tường đến chân thang là đoạn AB với độ dài là x
Ta có cos $\alpha$ = $\frac{x}{3}$ => x = 3.cos $\alpha$
Ta có cos $\alpha$ = $\frac{x}{3}$ => x = 3.cos $\alpha$
Vì $60^0$ $\leq$ $\alpha$ $\leq$ $70^0$
Nên cos $70^0$ $\leq$ cos $\alpha$ $\leq$ cos $60^0$
<=> 3.cos $70^0$ $\leq$ x $\leq$ cos 3.$60^0$
<=> 1,02 $\leq$ x $\leq$ 1,5
Vậy để an toàn chân thang phải đặt cách tường từ 1,02m đến 1,5m
Giải bài 43 trang 96 sgk hình học 9 tập 1
Bài giải:
Nếu gọi C là chu vi Trái đất, l là độ dài cung AS, $\alpha$ = $\widehat{AOS}$ thì:
C = $\frac{360^0}{\alpha}$.l
Các tia nắng mặt trời song song với nhau nên:
BC//OS
=> $\widehat{BCA}$ = $\widehat{AOS}$ = $\alpha$
Áp dụng tỉ số lượng giác đối với tam giác ABC vuông tại A, ta có:
tg $\alpha$ = $\frac{AB}{AC}$ = $\frac{3,1}{25}$ = 0,124
=> $\alpha$ $\approx$ $7^0$
Do đó: C = $\frac{360^0}{7^0}$.800 $\approx$ 41000.
Vậy chu vi Trái đất xấp xỉ 41000 (km)
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
EmoticonEmoticon