Giải bài luyện tập diện tích tam giác.
Nói về diện tích tam giác không đơn thuần chỉ là nhớ công thức, mà còn rất nhiều điều thú vị liên quan. Chẳng hạn, hai tam giác có diện tích bằng nhau thì có bằng nhau không. Ta cùng giải bài luyện tập về diện tích tam giác để khám phá những điều thú vị đó.
b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?
Bài giải:
a) Nếu lấy mỗi ô vuông làm đơn vị diện tích thì ta sẽ có diện tích của các tam giác trong hình 133 bằng:
$S_{\Delta 1}$ = $\frac{1}{2}$.2.4 = 4 (đvdt)
$S_{\Delta 2}$ = $\frac{1}{2}$.2.3 = 3 (đvdt)
$S_{\Delta 3}$ = $\frac{1}{2}$.2.4 = 4 (đvdt)
$S_{\Delta 4}$ = $\frac{1}{2}$.2.5 = 5 (đvdt)
$S_{\Delta 5}$ = $\frac{1}{2}$.3.3 = 4,5 (đvdt)
$S_{\Delta 6}$ = $\frac{1}{2}$.2.4 = 4 (đvdt)
$S_{\Delta 7}$ = $\frac{1}{2}$.1.7 = 3,5 (đvdt)
$S_{\Delta 8}$ = $\frac{1}{2}$.2.3 = 3 (đvdt)
Như vậy các tam giác có cùng diện tích là 1, 3, 6 và tam giác 2, 8.
b) Một điều dễ nhận thấy là hai tam giác có diện tích bằng nhau thì chưa chắc đã bằng nhau. Chẳng hạn, tam giác 1 và 3 có cùng diện tích là 4 nhưng hai tam giác đó không bằng nhau.
Bài giải:
Gọi tam giác cho trước là ABC với đường cao AH, E là trung điểm AH.
Ta sẽ vẽ hình chữ nhật BCDK với CD = MH.
Xét hai tam giác vuông AEN và BKN có:
AE = BK = $\frac{1}{2}$AH.
$\widehat{ANE}$ = $\widehat{BNK}$ (hai góc đối đỉnh)
Vậy $\Delta$ AEN = $\Delta$ BKN (cạnh góc vuông-góc nhọn)
Suy ra $S_{\Delta AEN}$ = $S_{\Delta BKN}$
Tương tự ta có:
$\widehat{AEM}$ = $\widehat{CDM}$.
Suy ra $S_{\Delta AEM}$ = $S_{\Delta CDM}$.
Khi đó $S_{\Delta BKN}$ + $S_{BNMC}$ + $S_{\Delta CDM}$ = $S_{\Delta AEN}$ + $S_{BNMC}$ + $S_{\Delta AEM}$
Hay $S_{BCDK}$ = $S_{\Delta ABC}$.
Mà $S_{BCDK}$ = CD.BC = EH.BC = $\frac{1}{2}$AH.BC
Vậy $S_{\Delta ABC}$ = $\frac{1}{2}$AH.BC.
Kết quả này cho chúng ta một cách chứng minh khác về diện tích tam giác.
Bài giải:
Theo công thức tính diện tích hình chữ nhật ta có:
$S_{ABCD}$ = AB.AD = x.AD = 5x.
Theo công thức tính diện tích tam giác ta có:
$S_{\Delta ADE}$ = $\frac{1}{2}$EH.AD = $\frac{1}{2}$2.5 = 5.
Diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE nghĩa là:
$S_{ABCD}$ = 3.$S_{\Delta ADE}$
<=> 5x = 3.5
<=> x = 3.
Vậy khi x = 3 thì diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE.
Hãy chỉ ra:
a) Một điểm I sao cho $S_{\Delta PIF}$ = $S_{\Delta PAF}$.
b) Một điểm O sao cho $S_{\Delta POF}$ = 2$S_{\Delta PAF}$.
c) Một điểm N sao cho $S_{\Delta PNF}$ = $\frac{1}{2}$$S_{\Delta PAF}$.
Bài giải:
a) Để $S_{\Delta PIF}$ = $S_{\Delta PAF}$, thì điểm I phải nằm trên đường thẳng a đi qua điểm A và song song với đường thẳng PF. Bởi khi đó hai tam giác có chung đáy PF và hai đường cao tương ứng bằng nhau.
Như vậy có vô số điểm I thỏa mãn điều kiện a)
b) Quan sát hình vẽ ta thấy điểm A cách cạnh PF 4 ô vuông. Do đó để $S_{\Delta POF}$ = 2$S_{\Delta PAF}$ thì điểm O phải cách PF một khoảng bằng 8 ô vuông. Khi đó điểm O sẽ thuộc đường thẳng b song song với đường thẳng PF và cách PF 8 ô vuông. Như vậy trong trường hợp này cũng có vô số điểm O thỏa mãn điều kiện.
c) Tương tự, điểm A cách PF một khoảng 4 ô vuông. Nên để $S_{\Delta PNF}$ = $\frac{1}{2}$$S_{\Delta PAF}$ thì điểm N phải cách PF 2 ô vuông. Nói cách khác điểm N nằm trên đường thẳng c song song với PF và cách PF một khoảng bằng 2 ô vuông. Có vô số điểm N như thế.
Qua ba trường hợp trên, ta rút ra một nhận xét: Tam giác ABC có cạnh BC cố định, diện tích của tam giác không đổi thì tập hợp các đỉnh A của tam giác là đường thẳng song song với BC cách BC một khoảng bằng đường cao AH của tam giác.
$S_{\Delta AMB}$ + $S_{\Delta BMC}$ = $S_{\Delta MAC}$.
Bài giải:
Giả sử điểm M nằm trong tam giác ABC như hình vẽ.
Ta có $S_{\Delta ABC}$ = $S_{\Delta AMB}$ + $S_{\Delta BMC}$ + $S_{\Delta MAC}$.
Mà $S_{\Delta AMB}$ + $S_{\Delta BMC}$ = $S_{\Delta MAC}$ (gt)
Nên $S_{\Delta ABC}$ = $S_{\Delta MAC}$ + $S_{\Delta MAC}$ = 2$S_{\Delta MAC}$
=> $S_{\Delta MAC}$ = $\frac{1}{2}$$S_{\Delta ABC}$.
<=> $\frac{1}{2}$.ME.AC = $\frac{1}{2}$.$\frac{1}{2}$.BH.AC
<=> ME = $\frac{1}{2}$.BH.
Điều đó có nghĩa là M nằm trên đường trung bình KN của tam giác ABC.
Bài giải:
Gọi tam giác đó là ABC với AB = AC = b, BC = a. Vẽ đường cao AH.
Ta có tam giác ABC cân tại A nên đường cao AH cũng là trung tuyến.
Khi đó HB = HC = $\frac{1}{2}$BC = $\frac{a}{2}$.
Áp dụng định lí Pi-ta-go vào tam giác vuông AHB, ta có:
$AB^2$ = $AH^2$ + $HB^2$
<=> $AH^2$ = $AB^2$ - $HB^2$
<=> $AH^2$ = $b^2$ - $(\frac{a}{2})^2$ = $b^2$ - $\frac{a^2}{4}$ = $\frac{4b^2 - a^2}{4}$.
<=> AH = $\sqrt{\frac{4b^2 - a^2}{4}}$ = $\frac{1}{2}$.$\sqrt{4b^2 - a^2}$.
Ta có $S_{\Delta ABC}$ = $\frac{1}{2}$.BC.AH = $\frac{1}{2}$.a.$\frac{1}{2}$.$\sqrt{4b^2 - a^2}$ = $\frac{a}{4}$.$\sqrt{4b^2 - a^2}$.
Vậy diện tích của một tam giác cân bằng $\frac{a}{4}$.$\sqrt{4b^2 - a^2}$ (đvdt).
Bài giải:
Tương tự bài 24, vẽ đường cao AH. Áp dụng định lí Pi-ta-go vào tam giác AHC, ta tính được:
AH = $\frac{a\sqrt{3}}{2}$
Ta có $S_{\Delta ABC}$ = $\frac{1}{2}$.BC.AH = $\frac{1}{2}$.a.$\frac{a\sqrt{3}}{2}$ = $\frac{a^2\sqrt{3}}{4}$
Vậy tam giác đều cạnh là a có diện tích bằng $\frac{a^2\sqrt{3}}{4}$ (đvdt).
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài 19 trang 122 sgk hình học 8 tập 1.
a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích)b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?
Bài giải:
 |
| Hình 133. |
a) Nếu lấy mỗi ô vuông làm đơn vị diện tích thì ta sẽ có diện tích của các tam giác trong hình 133 bằng:
$S_{\Delta 1}$ = $\frac{1}{2}$.2.4 = 4 (đvdt)
$S_{\Delta 2}$ = $\frac{1}{2}$.2.3 = 3 (đvdt)
$S_{\Delta 3}$ = $\frac{1}{2}$.2.4 = 4 (đvdt)
$S_{\Delta 4}$ = $\frac{1}{2}$.2.5 = 5 (đvdt)
$S_{\Delta 5}$ = $\frac{1}{2}$.3.3 = 4,5 (đvdt)
$S_{\Delta 6}$ = $\frac{1}{2}$.2.4 = 4 (đvdt)
$S_{\Delta 7}$ = $\frac{1}{2}$.1.7 = 3,5 (đvdt)
$S_{\Delta 8}$ = $\frac{1}{2}$.2.3 = 3 (đvdt)
Như vậy các tam giác có cùng diện tích là 1, 3, 6 và tam giác 2, 8.
b) Một điều dễ nhận thấy là hai tam giác có diện tích bằng nhau thì chưa chắc đã bằng nhau. Chẳng hạn, tam giác 1 và 3 có cùng diện tích là 4 nhưng hai tam giác đó không bằng nhau.
Giải bài 20 trang 122 sgk hình học 8 tập 1.
Vẽ hình chữ nhật có một cạnh bằng một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về diện tích tam giác.Bài giải:
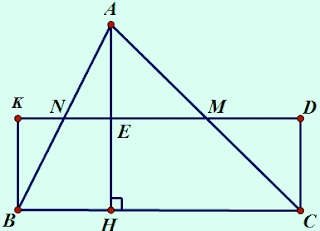 |
| Diện tích hình chữ nhật bằng diện tích tam giác. |
Ta sẽ vẽ hình chữ nhật BCDK với CD = MH.
Xét hai tam giác vuông AEN và BKN có:
AE = BK = $\frac{1}{2}$AH.
$\widehat{ANE}$ = $\widehat{BNK}$ (hai góc đối đỉnh)
Vậy $\Delta$ AEN = $\Delta$ BKN (cạnh góc vuông-góc nhọn)
Suy ra $S_{\Delta AEN}$ = $S_{\Delta BKN}$
Tương tự ta có:
$\widehat{AEM}$ = $\widehat{CDM}$.
Suy ra $S_{\Delta AEM}$ = $S_{\Delta CDM}$.
Khi đó $S_{\Delta BKN}$ + $S_{BNMC}$ + $S_{\Delta CDM}$ = $S_{\Delta AEN}$ + $S_{BNMC}$ + $S_{\Delta AEM}$
Hay $S_{BCDK}$ = $S_{\Delta ABC}$.
Mà $S_{BCDK}$ = CD.BC = EH.BC = $\frac{1}{2}$AH.BC
Vậy $S_{\Delta ABC}$ = $\frac{1}{2}$AH.BC.
Kết quả này cho chúng ta một cách chứng minh khác về diện tích tam giác.
Giải bài 21 trang 122 sgk hình học 8 tập 1.
Tính x sao cho diện tích hình chữ nhật ABCD gấp ba lần diện tích tam giác ADE (h134).Bài giải:
 |
| Hình 134. |
Theo công thức tính diện tích hình chữ nhật ta có:
$S_{ABCD}$ = AB.AD = x.AD = 5x.
Theo công thức tính diện tích tam giác ta có:
$S_{\Delta ADE}$ = $\frac{1}{2}$EH.AD = $\frac{1}{2}$2.5 = 5.
Diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE nghĩa là:
$S_{ABCD}$ = 3.$S_{\Delta ADE}$
<=> 5x = 3.5
<=> x = 3.
Vậy khi x = 3 thì diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE.
Giải bài 22 trang 122 sgk hình học 8 tập 1.
Tam giác PAF được vẽ trên giấy kẻ ô vuông (h135).Hãy chỉ ra:
a) Một điểm I sao cho $S_{\Delta PIF}$ = $S_{\Delta PAF}$.
b) Một điểm O sao cho $S_{\Delta POF}$ = 2$S_{\Delta PAF}$.
c) Một điểm N sao cho $S_{\Delta PNF}$ = $\frac{1}{2}$$S_{\Delta PAF}$.
Bài giải:
 |
| Hình 135. |
a) Để $S_{\Delta PIF}$ = $S_{\Delta PAF}$, thì điểm I phải nằm trên đường thẳng a đi qua điểm A và song song với đường thẳng PF. Bởi khi đó hai tam giác có chung đáy PF và hai đường cao tương ứng bằng nhau.
Như vậy có vô số điểm I thỏa mãn điều kiện a)
b) Quan sát hình vẽ ta thấy điểm A cách cạnh PF 4 ô vuông. Do đó để $S_{\Delta POF}$ = 2$S_{\Delta PAF}$ thì điểm O phải cách PF một khoảng bằng 8 ô vuông. Khi đó điểm O sẽ thuộc đường thẳng b song song với đường thẳng PF và cách PF 8 ô vuông. Như vậy trong trường hợp này cũng có vô số điểm O thỏa mãn điều kiện.
c) Tương tự, điểm A cách PF một khoảng 4 ô vuông. Nên để $S_{\Delta PNF}$ = $\frac{1}{2}$$S_{\Delta PAF}$ thì điểm N phải cách PF 2 ô vuông. Nói cách khác điểm N nằm trên đường thẳng c song song với PF và cách PF một khoảng bằng 2 ô vuông. Có vô số điểm N như thế.
Qua ba trường hợp trên, ta rút ra một nhận xét: Tam giác ABC có cạnh BC cố định, diện tích của tam giác không đổi thì tập hợp các đỉnh A của tam giác là đường thẳng song song với BC cách BC một khoảng bằng đường cao AH của tam giác.
Giải bài 23 trang 123 sgk hình học 8 tập 1.
Cho tam giác ABC. Hãy chỉ ra một số vị trí điểm M nằm trong tam giác đó sao cho:$S_{\Delta AMB}$ + $S_{\Delta BMC}$ = $S_{\Delta MAC}$.
Bài giải:
Giả sử điểm M nằm trong tam giác ABC như hình vẽ.
 |
| Tìm vị trí điểm M. |
Mà $S_{\Delta AMB}$ + $S_{\Delta BMC}$ = $S_{\Delta MAC}$ (gt)
Nên $S_{\Delta ABC}$ = $S_{\Delta MAC}$ + $S_{\Delta MAC}$ = 2$S_{\Delta MAC}$
=> $S_{\Delta MAC}$ = $\frac{1}{2}$$S_{\Delta ABC}$.
<=> $\frac{1}{2}$.ME.AC = $\frac{1}{2}$.$\frac{1}{2}$.BH.AC
<=> ME = $\frac{1}{2}$.BH.
Điều đó có nghĩa là M nằm trên đường trung bình KN của tam giác ABC.
Giải bài 24 trang 123 sgk hình học 8 tập 1.
Tính diện tích của một tam giác cân biết cạnh đáy bằng a và cạnh bên bằng b.Bài giải:
Gọi tam giác đó là ABC với AB = AC = b, BC = a. Vẽ đường cao AH.
Ta có tam giác ABC cân tại A nên đường cao AH cũng là trung tuyến.
Khi đó HB = HC = $\frac{1}{2}$BC = $\frac{a}{2}$.
Áp dụng định lí Pi-ta-go vào tam giác vuông AHB, ta có:
$AB^2$ = $AH^2$ + $HB^2$
<=> $AH^2$ = $AB^2$ - $HB^2$
<=> $AH^2$ = $b^2$ - $(\frac{a}{2})^2$ = $b^2$ - $\frac{a^2}{4}$ = $\frac{4b^2 - a^2}{4}$.
<=> AH = $\sqrt{\frac{4b^2 - a^2}{4}}$ = $\frac{1}{2}$.$\sqrt{4b^2 - a^2}$.
Ta có $S_{\Delta ABC}$ = $\frac{1}{2}$.BC.AH = $\frac{1}{2}$.a.$\frac{1}{2}$.$\sqrt{4b^2 - a^2}$ = $\frac{a}{4}$.$\sqrt{4b^2 - a^2}$.
Vậy diện tích của một tam giác cân bằng $\frac{a}{4}$.$\sqrt{4b^2 - a^2}$ (đvdt).
Giải bài 25 trang 123 sgk hình học 8 tập 1.
Tính diện tích của một tam giác đều có cạnh bằng a.Bài giải:
Tương tự bài 24, vẽ đường cao AH. Áp dụng định lí Pi-ta-go vào tam giác AHC, ta tính được:
AH = $\frac{a\sqrt{3}}{2}$
Ta có $S_{\Delta ABC}$ = $\frac{1}{2}$.BC.AH = $\frac{1}{2}$.a.$\frac{a\sqrt{3}}{2}$ = $\frac{a^2\sqrt{3}}{4}$
Vậy tam giác đều cạnh là a có diện tích bằng $\frac{a^2\sqrt{3}}{4}$ (đvdt).
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon