Diện tích tam giác.
Ở cấp 1, ta đã được học về diện tích tam giác nhưng chỉ dừng lại ở việc áp dụng công thức một cách máy móc. Giờ đã lên lớp 8, ta sẽ chứng minh công thức tính diện tích tam giác đó. Và cái thắc mắc ngây ngô của ngày xưa vì sao diện tích tam giác lại được tính như vậy sẽ được làm sáng rõ. Thật là tuyệt vời!
Định lí
Ta vẫn còn nhớ cô giáo lớp 5 đã dạy muốn tính diện tích hình tam giác ta lấy độ dài đáy nhân với chiều cao rồi chia cho 2. Giờ đây, điều đó được nhắc lại với cái tên "pro" hơn, đó là định lí về diện tích tam giác và được phát biểu như sau:Diện tích của tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
$S_{\Delta}$ = $\frac{1}{2}$a.h
Nhiệm vụ bây giờ của chúng ta là phải đi chứng minh định lí đó. Rõ ràng so với lớp 5, giờ ta đã ở một "đẳng cấp" khác rồi. Như bất kỳ một bài chứng minh nào, đầu tiên, ta sẽ ghi GT và KL. Dĩ nhiên những em lớp 5 không biết GT, KL là gì đâu. Trước khi lên lớp 8, ta đã học lớp 7 rồi, nên việc ghi GT, KL với ta dễ như... lướt facebook. Không đùa nữa, tập trung học thôi!
GT $\Delta$ ABC có diện tích S
AH $\perp$ BC
KL $S_{\Delta ABC}$ = $\frac{1}{2}$BC.AH
Chứng minh: Ta sẽ chứng minh định lí trên ở cả ba trường hợp tam giác vuông, tam giác nhọn, tam giác tù.
a) Trường hợp góc B vuông. Khi đó điểm H trùng với điểm B và AH trùng AB (h.126a).
Ta có: S = $\frac{1}{2}$BC.AB
Hay S = $\frac{1}{2}$BC.AH (vì AB = AH)
b) Trường hợp góc B nhọn (điểm H nằm giữa hai điểm B và C h.126b).
Khi đó tam giác ABC được chia thành hai tam giác vuông BHA và CHA.
Nên $S_{\Delta ABC}$ = $S_{\Delta BHA}$ + $S_{\Delta CHA}$
$S_{\Delta ABC}$ = $\frac{1}{2}$BH.AH + $\frac{1}{2}$HC.AH
$S_{\Delta ABC}$ = $\frac{(BH + HC).AH}{2}$
$S_{\Delta ABC}$ = $\frac{1}{2}$BC.AH
c) Trường hợp góc B tù (điểm H nằm ngoài hai điểm B và C h.126c).
Khi đó ta có
$S_{\Delta ABC}$ = $S_{\Delta CHA}$ - $S_{\Delta BHA}$
$S_{\Delta ABC}$ = $\frac{1}{2}$CH.AH - $\frac{1}{2}$BH.AH
$S_{\Delta ABC}$ = $\frac{(CH - HB).AH}{2}$
$S_{\Delta ABC}$ = $\frac{1}{2}$BC.AH
Vậy trong mọi trường hợp diện tích tam giác luôn bằng nửa tích của một cạnh với đường cao tương ứng với nó.
Khi đó $S_{\Delta}$ = $S_{HCN}$ = a. $\frac{h}{2}$
Điều đó được giải thích như sau:
Quan sát hình vẽ
Ta có hai tam giác bằng nhau, giữ nguyên một tam giác, tam giác còn lại cắt thành ba mảnh như hình vẽ và ghép thành một hình chữ nhật với $S_1$, $S_2$, $S_3$ là diện tích các đa giác được kí hiệu trong hình vẽ. Dễ dàng nhận thấy:
$S_{HCN}$ = $S_1$ + $S_2$ + $S_3$
$S_{\Delta}$ = $S_1$ + $S_2$ + $S_3$
Suy ra $S_{HCN}$ = $S_{\Delta}$
Mà $S_{HCN}$ = a. $\frac{h}{2}$
Nên $S_{\Delta}$ = a. $\frac{h}{2}$
Đó là một cách chứng minh khác về diện tích tam giác từ diện tích hình chữ nhật.
- Các tính chất của diện tích đa giác.
- Công thức tính diện tích tam giác vuông hoặc công thức tính diện tích hình chữ nhật.
Qua bài học này, ta cần nắm được công thức tính diện tích tam giác, biết cách chứng minh định lí về diện tích tam giác trong cả ba trường hợp một cách chặt chẽ, trình bày gãy gọn, dễ hiểu. Và dĩ nhiên là phải biết vận dụng công thức tính diện tích tam giác trong việc giải bài tập.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
GT $\Delta$ ABC có diện tích S
AH $\perp$ BC
KL $S_{\Delta ABC}$ = $\frac{1}{2}$BC.AH
Chứng minh: Ta sẽ chứng minh định lí trên ở cả ba trường hợp tam giác vuông, tam giác nhọn, tam giác tù.
a) Trường hợp góc B vuông. Khi đó điểm H trùng với điểm B và AH trùng AB (h.126a).
 |
| Hình 126a. Góc B vuông. |
Hay S = $\frac{1}{2}$BC.AH (vì AB = AH)
b) Trường hợp góc B nhọn (điểm H nằm giữa hai điểm B và C h.126b).
 |
| Hình 126b. Góc B nhọn, |
Nên $S_{\Delta ABC}$ = $S_{\Delta BHA}$ + $S_{\Delta CHA}$
$S_{\Delta ABC}$ = $\frac{1}{2}$BH.AH + $\frac{1}{2}$HC.AH
$S_{\Delta ABC}$ = $\frac{(BH + HC).AH}{2}$
$S_{\Delta ABC}$ = $\frac{1}{2}$BC.AH
c) Trường hợp góc B tù (điểm H nằm ngoài hai điểm B và C h.126c).
 |
| Hình 126c. Góc B tù. |
$S_{\Delta ABC}$ = $S_{\Delta CHA}$ - $S_{\Delta BHA}$
$S_{\Delta ABC}$ = $\frac{1}{2}$CH.AH - $\frac{1}{2}$BH.AH
$S_{\Delta ABC}$ = $\frac{(CH - HB).AH}{2}$
$S_{\Delta ABC}$ = $\frac{1}{2}$BC.AH
Vậy trong mọi trường hợp diện tích tam giác luôn bằng nửa tích của một cạnh với đường cao tương ứng với nó.
Tìm hiểu cách chứng minh khác về diện tích tam giác.
Quan sát hình 127, ta nhận thấy hình chữ nhật có độ dài một cạnh bằng cạnh đáy của tam giác, cạnh kề với nó bằng nửa đường cao tương ứng của tam giác.Khi đó $S_{\Delta}$ = $S_{HCN}$ = a. $\frac{h}{2}$
Điều đó được giải thích như sau:
Quan sát hình vẽ
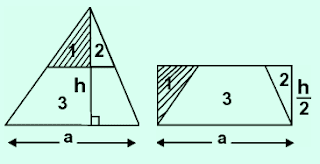 |
| Cách chứng minh khác. |
$S_{HCN}$ = $S_1$ + $S_2$ + $S_3$
$S_{\Delta}$ = $S_1$ + $S_2$ + $S_3$
Suy ra $S_{HCN}$ = $S_{\Delta}$
Mà $S_{HCN}$ = a. $\frac{h}{2}$
Nên $S_{\Delta}$ = a. $\frac{h}{2}$
Đó là một cách chứng minh khác về diện tích tam giác từ diện tích hình chữ nhật.
Xem lại: Công thức tính diện tích hình chữ nhật.Như vậy, cơ sở để chứng minh công thức tính diện tích của tam giác là:
- Các tính chất của diện tích đa giác.
- Công thức tính diện tích tam giác vuông hoặc công thức tính diện tích hình chữ nhật.
Qua bài học này, ta cần nắm được công thức tính diện tích tam giác, biết cách chứng minh định lí về diện tích tam giác trong cả ba trường hợp một cách chặt chẽ, trình bày gãy gọn, dễ hiểu. Và dĩ nhiên là phải biết vận dụng công thức tính diện tích tam giác trong việc giải bài tập.
Xem bài trước: Giải bài luyện tập diện tích hình chữ nhật.

EmoticonEmoticon