Giải SBT toán 8 hình thang.
Sau khi giải xong những bài tập SGK về hình thang, ta cứ tưởng những hiểu biết về hình thang như vậy là đã đầy đủ. Nhưng không phải vậy, các bạn thử hoàn thành các bài tập về hình thang trong SBT dưới đây, sẽ nhận ra rằng sự hiểu biết của chúng ta là có hạn. Và vì thế mà chúng ta luôn phải rèn luyện hằng ngày, "cặm cụi" giải tất cả những bài tập liên quan đến kiến thức cô giáo đã truyền dạy trên lớp thì may ra ta mới có thể giữ lại được một chút gì đó cho riêng mình, còn nếu không, những lời cô giảng sẽ theo... tiếng trống trường bay mất.
Bài giải:
Bài này hôm trước đã giải do có bạn yêu cầu. Nên giờ ta có thể xem bài giải ở đây.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài 11 trang 81 SBT toán 8 tập 1.
Tính các góc của hình thang ABCD (AB // CD), biết rằng $\widehat{A}$ = 3$\widehat{D}$, $\widehat{B}$ - $\widehat{C}$ = $30^0$Bài giải:
Bài này hôm trước đã giải do có bạn yêu cầu. Nên giờ ta có thể xem bài giải ở đây.
Giải bài 12 trang 81 SBT toán 8 tập 1.
Tứ giác ABCD có BC = CD và BD là tia phân giác của góc D. Chứng minh rằng ABCD là hình thang.
Bài giải:
Theo dấu hiệu nhận biết hình thang thì một tứ giác có hai cạnh song song là hình thang. Và như vậy ta phải lục lại cách chứng minh hai đường thẳng song song.
Ta có BC = CD nên tam giác BCD cân tại C
Suy ra $\widehat{B_1}$ = $\widehat{D_1}$
Ta lại có $\widehat{D_1}$ = $\widehat{D_2}$ (BD là tia phân giác của góc D)
Do đó $\widehat{B_1}$ = $\widehat{D_2}$
Mà hai góc $\widehat{B_1}$ và $\widehat{D_2}$ ở vị trí so le trong.
Suy ra BC // AD
Vậy tứ giác ABCD là hình thang. (đpcm)
 |
| BD là tia phân giác của góc D. |
Ta có BC = CD nên tam giác BCD cân tại C
Suy ra $\widehat{B_1}$ = $\widehat{D_1}$
Ta lại có $\widehat{D_1}$ = $\widehat{D_2}$ (BD là tia phân giác của góc D)
Do đó $\widehat{B_1}$ = $\widehat{D_2}$
Mà hai góc $\widehat{B_1}$ và $\widehat{D_2}$ ở vị trí so le trong.
Suy ra BC // AD
Vậy tứ giác ABCD là hình thang. (đpcm)
Giải bài 13 trang 81 SBT toán 8 tập 1.
Dùng thước và êke kiểm tra xem trong các tứ giác trên hình 2 SBT:
a) Tứ giác nào chỉ có một cặp cạnh song song.
b) Tứ giác nào có hai cặp cạnh song song.
c) Tứ giác nào là hình thang.
Bài giải:
Nhắc lại một chút về cách dùng thước và êke để kiểm tra hai đường thẳng có song song với nhau không:
- Đặt một cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra;
- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke;
- Điều chỉnh êke xem cạnh góc vuông có trùng với cạnh còn lại không. Nếu chúng trùng nhau thì hai cạnh đó song song.
 |
| Tứ giác nào là hình thang. |
Nhắc lại một chút về cách dùng thước và êke để kiểm tra hai đường thẳng có song song với nhau không:
- Đặt một cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra;
- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke;
- Điều chỉnh êke xem cạnh góc vuông có trùng với cạnh còn lại không. Nếu chúng trùng nhau thì hai cạnh đó song song.
Theo đó ta có kết quả như sau:
a) Tứ giác 1 chỉ có một cặp cạnh song song.
b) Tứ giác 3 có hai cặp cạnh song song.
c) Tứ giác 1 và 3 là hình thang.
a) Tứ giác 1 chỉ có một cặp cạnh song song.
b) Tứ giác 3 có hai cặp cạnh song song.
c) Tứ giác 1 và 3 là hình thang.
Giải bài 14 trang 81 SBT toán 8 tập 1.
Tính các góc B và D của hình thang ABCD, biết rằng $\widehat{A}$ = $60^0$, $\widehat{C}$ = $130^0$.
Bài giải:
Với hình thang ABCD thì $\widehat{A}$ và $\widehat{C}$ chính là hai góc đối. Nên sẽ có hai trường hợp xảy ra:
- Nếu $\widehat{A}$ và $\widehat{B}$ là hai góc kề một cạnh bên AB (xem hình bên dưới)
Khi đó ta có $\widehat{A}$ + $\widehat{B}$ = $180^0$
Mà $\widehat{A}$ = $60^0$
Suy ra $\widehat{B}$ = $120^0$ và tương tự $\widehat{D}$ = $50^0$.
- Nếu $\widehat{A}$ và $\widehat{D}$ là hai góc kề một cạnh bên như hình bên dưới thì khi đó $\widehat{B}$ = $50^0$ và $\widehat{D}$ = $130^0$.
Với hình thang ABCD thì $\widehat{A}$ và $\widehat{C}$ chính là hai góc đối. Nên sẽ có hai trường hợp xảy ra:
- Nếu $\widehat{A}$ và $\widehat{B}$ là hai góc kề một cạnh bên AB (xem hình bên dưới)
Khi đó ta có $\widehat{A}$ + $\widehat{B}$ = $180^0$
Mà $\widehat{A}$ = $60^0$
Suy ra $\widehat{B}$ = $120^0$ và tương tự $\widehat{D}$ = $50^0$.
 |
| A và B là hai góc kề cạnh bên AB. |
 |
| A và D là hai góc kề cạnh bên AD. |
Giải bài 15 trang 81 SBT toán 8 tập 1.
Chứng minh rằng trong hình thang có nhiều nhất là hai góc tù, có nhiều nhất là hai góc nhọn.
Bài giải:
Giả sử ta có hình thang ABCD với AB // CD.
Khi đó $\widehat{A}$ và $\widehat{D}$ là hai góc kề cạnh bên AD.
Mà hai góc kề một cạnh bên bù nhau tức có tổng bằng $180^0$. Trong hai góc đó nếu góc này nhọn thì góc kia sẽ là góc tù và ngược lại.
Do đó trong hai góc $\widehat{A}$ và $\widehat{D}$ có nhiều nhất là một góc nhọn và nhiều nhất là một góc tù. (1)
Tương tự, kề cạnh bên còn lại sẽ là hai góc $\widehat{B}$ và $\widehat{C}$. Trong hai góc $\widehat{B}$ và $\widehat{C}$ cũng có nhiều nhất là một góc nhọn và nhiều nhất là một góc tù. (2)
Từ (1) và (2) ta có trong bốn góc của hình thang ABCD có nhiều nhất là hai góc nhọn, nhiều nhất là hai góc tù (đpcm)
Giả sử ta có hình thang ABCD với AB // CD.
Khi đó $\widehat{A}$ và $\widehat{D}$ là hai góc kề cạnh bên AD.
Mà hai góc kề một cạnh bên bù nhau tức có tổng bằng $180^0$. Trong hai góc đó nếu góc này nhọn thì góc kia sẽ là góc tù và ngược lại.
Do đó trong hai góc $\widehat{A}$ và $\widehat{D}$ có nhiều nhất là một góc nhọn và nhiều nhất là một góc tù. (1)
Tương tự, kề cạnh bên còn lại sẽ là hai góc $\widehat{B}$ và $\widehat{C}$. Trong hai góc $\widehat{B}$ và $\widehat{C}$ cũng có nhiều nhất là một góc nhọn và nhiều nhất là một góc tù. (2)
Từ (1) và (2) ta có trong bốn góc của hình thang ABCD có nhiều nhất là hai góc nhọn, nhiều nhất là hai góc tù (đpcm)
Giải bài 16 trang 81 SBT toán 8 tập 1.
Chứng minh rằng trong hình thang, các tia phân giác của hai góc kề một cạnh bên vuông góc với nhau.
Bài giải:
Giả sử ta có hình thang ABCD với AB // CD, AE là tia phân giác của góc A, DE là tia phân giác của góc D.
Khi đó:
$\widehat{A_1}$ = $\widehat{A_2}$ = $\frac{A}{2}$ (AE là tia phân giác của góc A)
$\widehat{D_1}$ = $\widehat{D_2}$ = $\frac{D}{2}$ (DE là tia phân giác của góc D)
Suy ra $\widehat{A_1}$ + $\widehat{D_1}$ = $\frac{A + D}{2}$
Mà $\widehat{A}$ + $\widehat{D}$ = $180^0$ (hai góc kề một cạnh bên)
Nên $\widehat{A_1}$ + $\widehat{D_1}$ = $\frac{180^0}{2}$
<=> $\widehat{A_1}$ + $\widehat{D_1}$ = $90^0$
Tam giác ADE có $\widehat{A_1}$ + $\widehat{D_1}$ = $90^0$, suy ra $\widehat{AED}$ = $90^0$ (theo tổng ba góc của một tam giác)
Vậy AE $\perp$ DE (đpcm)
 |
| Chứng minh AE vuông góc với DE. |
Khi đó:
$\widehat{A_1}$ = $\widehat{A_2}$ = $\frac{A}{2}$ (AE là tia phân giác của góc A)
$\widehat{D_1}$ = $\widehat{D_2}$ = $\frac{D}{2}$ (DE là tia phân giác của góc D)
Suy ra $\widehat{A_1}$ + $\widehat{D_1}$ = $\frac{A + D}{2}$
Mà $\widehat{A}$ + $\widehat{D}$ = $180^0$ (hai góc kề một cạnh bên)
Nên $\widehat{A_1}$ + $\widehat{D_1}$ = $\frac{180^0}{2}$
<=> $\widehat{A_1}$ + $\widehat{D_1}$ = $90^0$
Tam giác ADE có $\widehat{A_1}$ + $\widehat{D_1}$ = $90^0$, suy ra $\widehat{AED}$ = $90^0$ (theo tổng ba góc của một tam giác)
Vậy AE $\perp$ DE (đpcm)
Giải bài 17 trang 81 SBT toán 8 tập 1.
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC cắt cạnh AB và AC ở D và E.
a) Tìm các hình thang trong hình vẽ.
b) Chứng minh rằng hình thang ABCD có một cạnh đáy bằng tổng hai cạnh bên.
Bài giải:
a) Ta vẽ hình theo yêu cầu của đề. Nhìn vào hình vẽ ta thấy có 3 hình thang, đó là: BDEC, BDIC, BIEC.
b) Theo đó ta sẽ chứng minh DE = BD + CE.
Ta có DE // BC (gt)
Do đó $\widehat{I_1}$ = $\widehat{B_1}$ (hai góc so le trong)
Mà $\widehat{B_1}$ = $\widehat{B_2}$ (BI là tia phân giác góc B)
Nên $\widehat{I_1}$ = $\widehat{B_2}$.
Vậy tam giác BDI cân tại D.
Suy ra DI = BD (1)
Tương tự ta có $\widehat{I_2}$ = $\widehat{C_1}$ (hai góc so le trong)
Mà $\widehat{C_1}$ = $\widehat{C_2}$ (CI là tia phân giác góc B)
Nên $\widehat{I_2}$ = $\widehat{C_2}$.
Vậy tam giác CEI cân tại E.
Suy ra IE = CE (2)
Cộng (1) và (2) vế theo vế ta được:
DI + IE = BD + CE
Hay DE = BD + CE (đpcm).
 |
| Các tia phân giác của góc B và C cắt nhau ở I. |
b) Theo đó ta sẽ chứng minh DE = BD + CE.
Ta có DE // BC (gt)
Do đó $\widehat{I_1}$ = $\widehat{B_1}$ (hai góc so le trong)
Mà $\widehat{B_1}$ = $\widehat{B_2}$ (BI là tia phân giác góc B)
Nên $\widehat{I_1}$ = $\widehat{B_2}$.
Vậy tam giác BDI cân tại D.
Suy ra DI = BD (1)
Tương tự ta có $\widehat{I_2}$ = $\widehat{C_1}$ (hai góc so le trong)
Mà $\widehat{C_1}$ = $\widehat{C_2}$ (CI là tia phân giác góc B)
Nên $\widehat{I_2}$ = $\widehat{C_2}$.
Vậy tam giác CEI cân tại E.
Suy ra IE = CE (2)
Cộng (1) và (2) vế theo vế ta được:
DI + IE = BD + CE
Hay DE = BD + CE (đpcm).
Giải bài 18 trang 82 SBT toán 8 tập 1.
Cho tam giác ABC vuông cân tại A. Ở phía ngoài tam giác ABC, vẽ tam giác BCD vuông cân tại B. Tứ giác ABDC là hình gì? Vì sao?
Bài giải:
Theo yêu cầu của đề ta có hình vẽ như sau:
Khi đó ta có $\widehat{C_1}$ = $45^0$ (vì tam giác ABC vuông cân tại A)
Ta lại có tam giác BCD vuông cân tại B nên $\widehat{C_2}$ = $45^0$
Do đó $\widehat{C}$ = $90^0$ (1)
Nên CD $\perp$ AC
Mặt khác ta cũng có AB $\perp$ AC (vì $\widehat{A}$ = $90^0$)
Suy ra AB // CD. (2)
Từ (1) và (2) suy ra tứ giác ABDC là hình thang vuông. (đpcm)
Theo yêu cầu của đề ta có hình vẽ như sau:
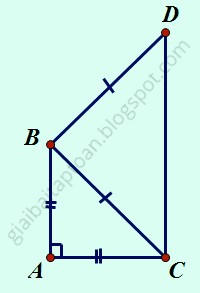 |
| Tứ giác ABDC là hình gì? |
Ta lại có tam giác BCD vuông cân tại B nên $\widehat{C_2}$ = $45^0$
Do đó $\widehat{C}$ = $90^0$ (1)
Nên CD $\perp$ AC
Mặt khác ta cũng có AB $\perp$ AC (vì $\widehat{A}$ = $90^0$)
Suy ra AB // CD. (2)
Từ (1) và (2) suy ra tứ giác ABDC là hình thang vuông. (đpcm)
Giải bài 19 trang 82 SBT toán 8 tập 1.
Hình thang vuông ABCD có $\widehat{A}$ = $\widehat{D}$ = $90^0$, AB = AD = 2cm, DC = 4cm. Tính các góc của hình thang.
Bài giải:
Hình thang vuông ABCD, đã có $\widehat{A}$ = $\widehat{D}$ = $90^0$ rồi. Nên ta chỉ tìm cách để tính hai góc còn lại thôi. Nghe có vẻ dễ, nhưng cứ loay hoay mãi cho đến khi thử kẻ BK $\perp$ DC, thì cách giải bài toán mới được định hình.
Kẻ BK $\perp$ DC, khi đó hình thang ABCD có hai cạnh bên song song nên:
AD = BK, AB = DK
Mà theo gt AB = AD = 2cm
Suy ra BK = DK = 2cm. (1)
Ta có DK + KC = DC
<=> KC = DC - DK = 4 - 2 = 2 cm. (2)
Từ (1) và (2) suy ra BK = KC
Do đó tam giác BKC cân tại K.
Suy ra $\widehat{C}$ = $45^0$
$\widehat{B}$ và $\widehat{C}$ là hai góc kề cạnh bên BC nên dễ dàng suy ra:
$\widehat{B}$ = $180^0$ - $\widehat{C}$ = $180^0$ - $45^0$ = $135^0$.
Vậy $\widehat{C}$ = $45^0$, $\widehat{B}$ = $135^0$.
Hình thang vuông ABCD, đã có $\widehat{A}$ = $\widehat{D}$ = $90^0$ rồi. Nên ta chỉ tìm cách để tính hai góc còn lại thôi. Nghe có vẻ dễ, nhưng cứ loay hoay mãi cho đến khi thử kẻ BK $\perp$ DC, thì cách giải bài toán mới được định hình.
 |
| Tính các góc của hình thang. |
AD = BK, AB = DK
Mà theo gt AB = AD = 2cm
Suy ra BK = DK = 2cm. (1)
Ta có DK + KC = DC
<=> KC = DC - DK = 4 - 2 = 2 cm. (2)
Từ (1) và (2) suy ra BK = KC
Do đó tam giác BKC cân tại K.
Suy ra $\widehat{C}$ = $45^0$
$\widehat{B}$ và $\widehat{C}$ là hai góc kề cạnh bên BC nên dễ dàng suy ra:
$\widehat{B}$ = $180^0$ - $\widehat{C}$ = $180^0$ - $45^0$ = $135^0$.
Vậy $\widehat{C}$ = $45^0$, $\widehat{B}$ = $135^0$.
Giải bài 20 trang 82 SBT toán 8 tập 1.
Chứng minh rằng tổng hai cạnh bên của hình thang lớn hơn hiệu hai đáy.
Bài giải:
Giả sử ta có hình thang ABCD (AB // CD, AB < CD), ta sẽ phải chứng minh AD + BC > CD - AB
Kẻ BF // AD.
Lúc này hình thang ABCD có hai cạnh bên song song nên:
BF = AD và AB = DF
Khi đó AD + BC = BF + BC (1)
CD - AB = CD - DF
Mà CD - DF = CF
Nên CD - AB = CF (2)
Xét tam giác BFC có BF + BC > CF (3)
Từ (1) (2) và (3) suy ra AD + BC > CD - AB. (đpcm)
Giả sử ta có hình thang ABCD (AB // CD, AB < CD), ta sẽ phải chứng minh AD + BC > CD - AB
 |
| Chứng minh AD + BC > CD - AB. |
Lúc này hình thang ABCD có hai cạnh bên song song nên:
BF = AD và AB = DF
Khi đó AD + BC = BF + BC (1)
CD - AB = CD - DF
Mà CD - DF = CF
Nên CD - AB = CF (2)
Xét tam giác BFC có BF + BC > CF (3)
Từ (1) (2) và (3) suy ra AD + BC > CD - AB. (đpcm)
Giải bài 21 trang 82 SBT toán 8 tập 1.
Trong hình 3 có bao nhiêu hình thang?
Bài giải:
Ta sẽ viết tên các hình thang ra giấy và chỉ cần biết ... đếm nữa thôi là đã giải xong bài tập này!
Nhìn vào hình vẽ ta nhận ra rất nhiều hình thang với những cái tên rất đẹp! Để không "bỏ sót" hình nào, ta sẽ đọc từ trên xuống như sau:
ABCD, ABEF, ABGH, ABIK, DCEF, DCGH, DCIK, FEGH, FEIK, HGIK.
Sau khi "đếm đi đếm lại" ta chắc chắn một điều rằng có tất cả 10 hình thang.
Còn các bạn, các bạn đếm được bao nhiêu hình thang!
Ta sẽ viết tên các hình thang ra giấy và chỉ cần biết ... đếm nữa thôi là đã giải xong bài tập này!
 |
| Hình 3. |
ABCD, ABEF, ABGH, ABIK, DCEF, DCGH, DCIK, FEGH, FEIK, HGIK.
Sau khi "đếm đi đếm lại" ta chắc chắn một điều rằng có tất cả 10 hình thang.
Còn các bạn, các bạn đếm được bao nhiêu hình thang!
Xem bài trước: Giải SBT toán 8 về tứ giác.

EmoticonEmoticon