Giải bài tập về hình thang.

Giải bài tập về hình thang thì đương nhiên ta phải biết hình thang là hình như thế nào, có tính chất gì và dấu hiệu để nhận biết một hình thang... Tất cả đã được học trong bài hình thang, giờ chỉ cần "lấy ra" áp dụng để giải bài tập thôi. Và đến lượt "mình", những bài tập được giải, lại giúp ta nắm vững tất tần tật về hình thang.

Giải bài tập 6 trang 70 sgk hình 8 tập 1

Dùng thước kẻ và êke, ta có thể kiểm tra hai đường thẳng có song song với nhau hay không? (Xem hình 19 sgk). Trên hình 20 có những tứ giác là hình thang, có những tứ giác không là hình thang. Bằng cách nêu trên, kiểm tra xem trong các tứ giác ở hình 20, tứ giác nào là hình thang.

Bài giải:

Cách kiểm tra:

- Đặt mép cạnh góc vuông của êke trùng với một trong hai cạnh cần kiểm tra

- Đặt mép thước trùng với mép cạnh góc vuông còn lại của êke

- Điều chỉnh eke xem cạnh góc vuông có trùng với cạnh còn lại của tứ giác mà ta cần kiểm tra hay không. Nếu chúng trùng nhau thì tứ giác đó là hình thang.

Tứ giác nào là hình thang,

Bằng cách kiểm tra như trên:

- Với hình a, ta có AB//DC nên tứ giác ABCD là hình thang

- Với hình b, tứ giác GHEF không phải là hình thang

- Với hình c, ta có KM//IN nên tứ giác KMNI là hình thang.

Giải bài tập 7 trang 71 sgk hình 8 tập 1

Tìm x và y trên hình 21, biết rằng ABCD là hình thang có đáy là AB, CD

Bài giải:

Tìm x và y

a) Với hình 21a, ta có:

$\widehat{A}$ + $\widehat{D}$ = $180^0$ <=> x + $80^0$ = $180^0$ <=> x = $180^0$ - $80^0$ = $100^0$

$\widehat{C}$ + $\widehat{B}$ = $180^0$ <=> y + $40^0$ = $180^0$ <=> y = $180^0$ - $40^0$ = $140^0$

b) Với hình 21b, ta dễ dàng nhận thấy:

x = $70^0$ ( hai góc đồng vị)

y = $50^0$ (hai góc so le trong)

c) Với hình 21c, ta có:

$\begin{cases}AB//CD\\BC \perp CD\end{cases}$ => BC $\perp$ AB

Suy ra $\widehat{ABC}$ = $90^0$ hay x = $90^0$

$\widehat{A}$ + $\widehat{D}$ = $180^0$ <=> $65^0$ + y = $180^0$ <=> y = $180^0$ - $65^0$ = $115^0$

Giải bài tập 8 trang 71 sgk hình 8 tập 1

Hình thang ABCD (AB // CD) có $\widehat{A}$ - $\widehat{D}$ = $20^0$, $\widehat{B}$ = 2$\widehat{C}$. Tính các góc của hình thang.

Bài giải:

Ta có:

$\begin{cases}\widehat{A} + \widehat{D} = 180^0\\\widehat{A} - \widehat{D} = 20^0\end{cases}$ <=> 2$\widehat{A}$ = $200^0$ <=> $\widehat{A}$ = $100^0$

Suy ra $\widehat{D}$ = $80^0$

$\begin{cases}\widehat{B} + \widehat{C} = 180^0\\\widehat{B} = 2 \widehat{C}\end{cases}$ <=> 3$\widehat{C}$ = $180^0$  <=> $\widehat{C}$ = $60^0$

Suy ra $\widehat{B}$ = $120^0$

Giải bài tập 9 trang 71 sgk hình 8 tập 1

Tứ giác ABCD có AB = BC và AC là phân giác của góc A. Chứng minh rằng ABCD là hình thang.

Bài giải:

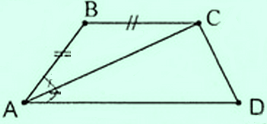AC là phân giác góc A

Ta có AB = BC nên tam giác ABC cân tại B

Suy ra $\widehat{BAC}$ = $\widehat{BCA}$     (1)

Mặt khác AC là phân giác của $\widehat{BAD}$ nên $\widehat{BAC}$ = $\widehat{DAC}$     (2)

Từ (1) và (2) suy ra $\widehat{BCA}$ = $\widehat{DAC}$

Do đó BC //AD

Nên tứ giác ABCD là hình thang (đpcm)

Giải bài tập 10 trang 71 sgk hình 8 tập 1

Đố. Hình 22 là hình vẽ một chiếc thang. Trên hình vẽ có bao nhiêu hình thang.

Bài giải:

Chiếc thang.

Bài này thật là dễ, ta chỉ việc đọc tên lên, rồi đếm là xong.
Có tất cả 6 hình thang: ABCD, CDEF, EFGH, ABEF, CDGH, ABGH.

Xem bài trước: Giải bài tập về tứ giác

Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

CÙNG CHIA SẺ ĐỂ KIẾN THỨC ĐƯỢC LAN TỎA!

Be a Fan

Bài học liên quan.