Giải SBT đường kính và dây của đường tròn.
Giải bài 15 trang 158 SBT toán 9 tập 1.
Cho tam giác ABC, các đường cao BH, CK. Chứng minh rằng:a) Bốn điểm B, C, H, K cùng thuộc một đường tròn.
b) HK < BC.
Bài giải:
a) Trong chương trình hình học lớp 8 ta đã được học một định lí trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền. Ta sẽ áp dụng định lí này để giải.
 |
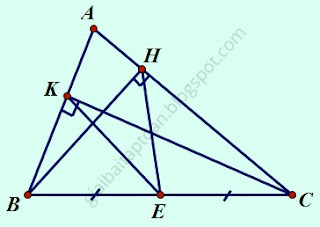| BH, CK là các đường cao tam giác ABC. |
BE = CE = $\frac{1}{2}$BC (1)
HE là trung tuyến của tam giác vuông BHC nên HE = $\frac{1}{2}$BC (2)
KE là trung tuyến của tam giác vuông BKC nên KE = $\frac{1}{2}$BC (3)
Từ (1) (2) (3) suy ra BE = CE = HE = KE
Do đó bốn điểm B, C, H, K cùng thuộc đường tròn tâm E bán kính EB (đpcm)
b) Xét đường tròn tâm E bán kính EB có
BC là đường kính
HK là dây cung
Theo định lí 1 trong các dây của đường tròn dây lớn nhất là đường kính.
Do đó HK < BC (đpcm)
Giải bài 16 trang 159 SBT toán 9 tập 1.
Tứ giác ABCD có $\widehat{B}$ = $\widehat{D}$ = $90^0$
a) Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn.
b) So sánh độ dài BD và AC. Nếu AC = BD thì tứ giác ABCD là hình gì?
Bài giải:
a) Gọi O là trung điểm của AC. Khi đó ta có:
AO = CO = $\frac{1}{2}$AC (1)BO là trung tuyến của tam giác vuông ABC nên BO = $\frac{1}{2}$AC (2)
DO là trung tuyến của tam giác vuông ADC nên DO = $\frac{1}{2}$AC (3)
Từ (1) (2) (3) suy ra AO = CO = BO = DO
Vậy bốn điểm A, B, C, D cùng thuộc đường tròn tâm O bán kính OA (đpcm)
 |
| Tứ giác ABCD là hình gì? |
AC = BD khi và chỉ khi BD cũng là đường kính. Khi đó tứ giác ABCD là hình chữ nhật.
Giải bài 19 trang 159 SBT toán 9 tập 1.
Cho đường tròn (O), đường kính AD = 2R. Vẽ cung tâm D bán kính R, cung này cắt đường tròn (O) ở B và C.
a) Tứ giác OBDC là hình gì? Vì sao?
b) Tính số đo các góc CBD, CBO, OBA
c) Chứng minh rằng tam giác ABC là tam giác đều.
Bài giải:
a) Ta có OB = OC = R (bán kính đường tròn O)
DB = DC = R (bán kính cung tròn tâm D)
Tứ giác OBDC có OB = OC = DB = DC nên OBDC là hình thoi.
 |
| Chứng minh tam giác ABC đều. |
b) Xét tam giác BOD có OB = OD = DB nên BOD là tam giác đều.
Suy ra $\widehat{OBD}$ = $60^0$
Ta có BC là đường chéo của hình thoi nên là đường phân giác góc DOB
Suy ra $\widehat{CBO}$ = $\widehat{CBD}$ = $\frac{\widehat{OBD}}{2}$ = $30^0$.
Ta có $\widehat{ABD}$ = $90^0$ (vì tam giác ABD nội tiếp đường tròn đường kính AD)
Khi đó $\widehat{OBA}$ = $\widehat{ABD}$ - $\widehat{OBD}$ = $90^0$ - $60^0$ = $30^0$
Vậy $\widehat{CBO}$ = $\widehat{CBD}$ = $30^0$, $\widehat{OBA}$ = $30^0$
c) Ta có $\widehat{ABC}$ = $\widehat{CBO}$ + $\widehat{OBA}$ = $30^0$ = $30^0$ + $30^0$ = $60^0$
Tính tương tự câu b) ta được $\widehat{BCO}$ = $30^0$, $\widehat{OCA}$ = $30^0$. Suy ra $\widehat{ACB}$ = $60^0$
Tam giác ABC có $\widehat{ABC}$ = $60^0$ và $\widehat{ACB}$ = $60^0$ nên ABC là tam giác đều.
Giải bài 20 trang 159 SBT toán 9 tập 1.
a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB tại M và N. Chứng minh rằng AM = BN
b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và qua N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.
Bài giải:
 |
| Chứng minh AM = BN |
Theo định lí 3 đường trung bình của hình thang thì hình thang CDNM có HC = HD và HO // CM // DN nên OM = ON.
Suy ra AM = BN (đpcm)
b) Gọi H là trung điểm của CD
 |
| Chứng minh MC, ND vuông góc với CD. |
Hình thang CDNM có OH là đường trung bình nên OH // MC // ND (1)
Mặc khác ta có OH $\perp$ CD (2) (đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy)
Từ (1) và (2) suy ra MC $\perp$ CD, ND $\perp$ CD (đpcm)
EmoticonEmoticon