Giải bài tập hình thoi.
Có một sự liên hệ đặc biệt giữa hình chữ nhật và hình thoi, đó là các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi và các trung điểm của bốn cạnh của một hình thoi lại là các đỉnh của một hình chữ nhật. Điều thú vị đó sẽ được chứng minh trong bài giải bài tập về hình thoi hôm nay.
Bài giải:
➤ Hình 102a:
theo định nghĩa tứ giác ABCD là hình thoi.
➤ Hình 102b: Tứ giác EFGH có các cạnh đối bằng nhau nên là hình bình hành. Mặt khác lại có EG là phân giác góc E => EFGH là hình bình hành.
➤ Hình 102c:
Ta có tứ giác KINM là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Mặt khác IM $\perp$ KN
Nên KINM là hình thoi.
➤ Hình 102d: PQRS không phải là hình thoi.
➤ Hình 102e:
Nối A với B, ta có: AD = BD = BC (vì cùng bằng AB = R)
=> ABCD là hình thoi (theo định nghĩa hình thoi)
(A) 6cm (B) $\sqrt{41}$cm (C) $\sqrt{164}$cm (D) 9cm?
Bài giải:
Ta biết hai đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên:
AC $\perp$ BD
OB = OD = 4cm
OA = OC = 5cm
AB = BC = CD = DA
Áp dụng định lí Pi-ta-go trong tam giác vuông BOC, ta có:
$BC^2$ = $OB^2$ + $OC^2$ = $4^2$ + $5^2$ = 16 + 25 = 41
=> BC = $\sqrt{41}$.
Vậy ta chọn phương án (B)
Bài giải:
Xét hai tam giác AEH và BEF có:
AH = BF = $\frac{AD}{2}$ = $\frac{BC}{2}$
$\widehat{A}$ = $\widehat{B}$ = $90^0$ (vì ABCD là hcn)
AE = BE = $\frac{AB}{2}$ (gt)
=> $\Delta$ AEH = $\Delta$ BEF (c-g-c)
=> EH = EF (hai cạnh tương ứng)
Chứng minh tương tự, ta được:
EF = GF = GH = EH
=> EFGH là hình thoi (theo định nghĩa hình thoi)
Bài giải:
Ta có MN là đường trung bình của tam giác BAC (gt)
Nên MN // AC và MN = $\frac{AC}{2}$ (1)
Tương tự, ta có PQ là đường trung bình của tam giác DAC nên:
PQ // AC và PQ = $\frac{AC}{2}$ (2)
Từ (1) và (2) suy ra MN // PQ và MN = PQ
Do đó tứ giác MNPQ là hình bình hành. (*)
Chứng minh tương tự, ta được MQ // BD (3)
Mà AC $\perp$ BD (4) (vì ABCD là hình thoi)
Từ (1), (3), (4) suy ra MN $\perp$ MQ (**)
Kết hợp (*) và (**) suy ra tứ giác MNPQ là hình chữ nhật (đpcm)
a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.
Bài giải:
a) Ta đã biết hình thoi là một hình bình hành đặc biệt, dĩ nhiên rồi, cô giáo đã dạy như thế. Mà ta cũng đã được học hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
Do đó giao điểm của hai đường chéo của hình thoi cũng là tâm đối xứng của nó (đpcm)
b) Xét hình thoi ABCD có:
A đối xứng với chính nó qua AC, B đối xứng với D qua AC. Suy ra AB đối xứng với AD qua AC.
Tương tự CB và CD cũng đối xứng với nhau qua AC.
Như vậy AC là trục đối xứng của hình thoi ABCD.
Một cách tương tự, ta cũng chứng minh được BD là trục đối xứng của hình thoi ABCD.
Vậy hai đường chéo của hình thoi là hai trục đối xứng của hình thoi (đpcm)
Bài giải:
Ta kí hiệu các điểm trên cửa xếp như hình vẽ.
Ta có ABCD là hình chữ nhật (tứ giác ABCD có các đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường)
Do đó CD // AB
Ta lại có IDKC là hình thoi (tứ giác có 4 cạnh bằng nhau)
Nên IK $\perp$ CD (hai đường chéo của hình thoi)
Suy ra IK $\perp$ AB (1) (vì CD // AB cmt)
Tương tự, ta có CDFE là hình chữ nhật.
Do đó EF // CD
Ta lại có KFME là hình thoi.
=> KM $\perp$ EF <=> KM $\perp$ CD (vì EF // CD)
Do đó KM $\perp$ AB (2) (vì AB // CD)
Từ (1) và (2) chứng tỏ I, K, M cùng thuộc đường thẳng vuông góc với AB.
Chứng minh tương tự, suy ra các chốt I, K, M, N, O luôn nằm trên một đường thẳng. Đường thẳng đó vuông góc với AB.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài 73 trang 105 sgk hình học 8 tập 1.
Tìm các hình thoi trên hình 102.Bài giải:
 |
| Hình 102. |
➤ Hình 102a:
theo định nghĩa tứ giác ABCD là hình thoi.
➤ Hình 102b: Tứ giác EFGH có các cạnh đối bằng nhau nên là hình bình hành. Mặt khác lại có EG là phân giác góc E => EFGH là hình bình hành.
➤ Hình 102c:
Ta có tứ giác KINM là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường.
Mặt khác IM $\perp$ KN
Nên KINM là hình thoi.
➤ Hình 102d: PQRS không phải là hình thoi.
➤ Hình 102e:
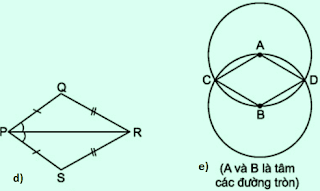 |
| Hình 102. |
=> ABCD là hình thoi (theo định nghĩa hình thoi)
Giải bài 74 trang 106 sgk hình học 8 tập 1.
Hai đường chéo của hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào sau đây:(A) 6cm (B) $\sqrt{41}$cm (C) $\sqrt{164}$cm (D) 9cm?
Bài giải:
Ta biết hai đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên:
AC $\perp$ BD
OB = OD = 4cm
OA = OC = 5cm
AB = BC = CD = DA
Áp dụng định lí Pi-ta-go trong tam giác vuông BOC, ta có:
$BC^2$ = $OB^2$ + $OC^2$ = $4^2$ + $5^2$ = 16 + 25 = 41
=> BC = $\sqrt{41}$.
Vậy ta chọn phương án (B)
Giải bài 75 trang 106 sgk hình học 8 tập 1.
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.Bài giải:
 |
| Trung điểm 4 cạnh hình chữ nhật. |
Xét hai tam giác AEH và BEF có:
AH = BF = $\frac{AD}{2}$ = $\frac{BC}{2}$
$\widehat{A}$ = $\widehat{B}$ = $90^0$ (vì ABCD là hcn)
AE = BE = $\frac{AB}{2}$ (gt)
=> $\Delta$ AEH = $\Delta$ BEF (c-g-c)
=> EH = EF (hai cạnh tương ứng)
Chứng minh tương tự, ta được:
EF = GF = GH = EH
=> EFGH là hình thoi (theo định nghĩa hình thoi)
Giải bài 76 trang 106 sgk hình học 8 tập 1.
Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.Bài giải:
 |
| Trung điểm 4 cạnh hình thoi. |
Ta có MN là đường trung bình của tam giác BAC (gt)
Nên MN // AC và MN = $\frac{AC}{2}$ (1)
Tương tự, ta có PQ là đường trung bình của tam giác DAC nên:
PQ // AC và PQ = $\frac{AC}{2}$ (2)
Từ (1) và (2) suy ra MN // PQ và MN = PQ
Do đó tứ giác MNPQ là hình bình hành. (*)
Chứng minh tương tự, ta được MQ // BD (3)
Mà AC $\perp$ BD (4) (vì ABCD là hình thoi)
Từ (1), (3), (4) suy ra MN $\perp$ MQ (**)
Kết hợp (*) và (**) suy ra tứ giác MNPQ là hình chữ nhật (đpcm)
Giải bài 77 trang 106 sgk hình học 8 tập 1.
Chứng minh rằng:a) Giao điểm hai đường chéo của hình thoi là tâm đối xứng của hình thoi.
b) Hai đường chéo của hình thoi là hai trục đối xứng của hình thoi.
Bài giải:
a) Ta đã biết hình thoi là một hình bình hành đặc biệt, dĩ nhiên rồi, cô giáo đã dạy như thế. Mà ta cũng đã được học hình bình hành có tâm đối xứng là giao điểm của hai đường chéo.
Do đó giao điểm của hai đường chéo của hình thoi cũng là tâm đối xứng của nó (đpcm)
b) Xét hình thoi ABCD có:
A đối xứng với chính nó qua AC, B đối xứng với D qua AC. Suy ra AB đối xứng với AD qua AC.
Tương tự CB và CD cũng đối xứng với nhau qua AC.
Như vậy AC là trục đối xứng của hình thoi ABCD.
Một cách tương tự, ta cũng chứng minh được BD là trục đối xứng của hình thoi ABCD.
Vậy hai đường chéo của hình thoi là hai trục đối xứng của hình thoi (đpcm)
Giải bài 78 trang 106 sgk hình học 8 tập 1.
Đố. Hình 103 biểu diễn một phần của cửa xếp, gồm những thanh kim loại dài bằng nhau và được liên kết với nhau bởi các chốt hai đầu và tại trung điểm. Vì sao tại mỗi vị trí của cửa xếp, các tứ giác trên hình vẽ đều là hình thoi, các điểm chốt I, K, M, N, O đều nằm trên một đường thẳng.Bài giải:
 |
| Hình 103. |
Ta kí hiệu các điểm trên cửa xếp như hình vẽ.
Ta có ABCD là hình chữ nhật (tứ giác ABCD có các đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường)
Do đó CD // AB
Ta lại có IDKC là hình thoi (tứ giác có 4 cạnh bằng nhau)
Nên IK $\perp$ CD (hai đường chéo của hình thoi)
Suy ra IK $\perp$ AB (1) (vì CD // AB cmt)
Tương tự, ta có CDFE là hình chữ nhật.
Do đó EF // CD
Ta lại có KFME là hình thoi.
=> KM $\perp$ EF <=> KM $\perp$ CD (vì EF // CD)
Do đó KM $\perp$ AB (2) (vì AB // CD)
Từ (1) và (2) chứng tỏ I, K, M cùng thuộc đường thẳng vuông góc với AB.
Chứng minh tương tự, suy ra các chốt I, K, M, N, O luôn nằm trên một đường thẳng. Đường thẳng đó vuông góc với AB.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon