Giải bài luyện tập trường hợp bằng nhau thứ hai cạnh góc cạnh.
Ta biết rằng nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau. Nhưng đôi khi hai tam giác có hai cặp cạnh và một cặp góc bằng nhau, nhưng hai tam giác đó vẫn không bằng nhau. Tại sao lại như thế nhỉ? Cùng giải bài luyện tập trường hợp bằng nhau thứ hai cạnh góc cạnh một lần nữa, ta sẽ hiểu vì sao lại như vậy!
a) $\Delta$ ABC = $\Delta$ ADC (h.86).
b) $\Delta$ AMB = $\Delta$ EMC (h.87).
c) $\Delta$ CAB = $\Delta$ DBA (h.88).
Bài giải:
a) Để $\Delta$ ABC = $\Delta$ ADC (c-g-c) cần thêm $\widehat{BAC}$ = $\widehat{DAC}$.
b) Để $\Delta$ AMB = $\Delta$ EMC (c-g-c) cần thêm MA = ME.
c) $\Delta$ CAB = $\Delta$ DBA (c-g-c) cần thêm AC = BD.
Bài giải:
Xét tam giác DKE có $\widehat{D}$ + $\widehat{K}$ + $\widehat{E}$ = $180^0$ (theo định lí tổng ba góc của một tam giác)
Mà $\widehat{K}$ = $80^0$, $\widehat{E}$ = $40^0$ (gt)
Suy ra $\widehat{D}$ = $60^0$
Xét hai tam giác ABC và KDE có:
AB = KD (gt)
$\widehat{B}$ = $\widehat{D}$ = $60^0$
BC = DE (gt)
Suy ra $\Delta$ ABC = $\Delta$ KDE (c-g-c)
Còn $\Delta$ MNP không bằng hai tam giác còn lại vì không có đủ các điều kiện c-c-c hoặc c-g-c.
Bài giải:
Ta có $\left.\begin{matrix} AB = AD\\ BE = DC\end{matrix}\right\}$ => AE = AC.
Xét hai tam giác ABC và ADE có:
AB = AD (gt)
$\widehat{A}$ chung.
AC = AE (cmt)
Suy ra $\Delta$ ABC = $\Delta$ ADE (c-g-c)
Bài giải:
Ta thấy:
$\widehat{ABC}$ không phải là góc xen giữa hai cạnh BC và CA
$\widehat{A'BC}$ không phải là góc xen giữa hai cạnh BC và CA'.
Nên không thể áp dụng trường hợp cạnh - góc - cạnh để kết luận $\Delta$ ABC = $\Delta$ A'BC
Bài giải:
Xét tam giác MIA và MIB có:
IA = IB (gt)
$\widehat{MIA}$ = $\widehat{MIB}$ = $90^0$ (gt)
Cạnh MI chung.
Nên $\Delta$ MIA = $\Delta$ MIB (c-g-c)
Suy ra MA = MB.
Bài giải:
Xét hai tam giác AHB và KHB có:
AH = KH (gt)
$\widehat{AHB}$ = $\widehat{KHB}$ = $90^0$ (gt)
Cạnh BH chung.
Do đó $\Delta$ AHB = $\Delta$ KHB (c-g-c)
Suy ra $\widehat{ABH}$ = $\widehat{KBH}$ (hai góc tương ứng)
Vậy tia BC là tia phân giác của góc ABK.
Xét hai tam giác AHC và KHC có:
AH = KH (gt)
$\widehat{AHC}$ = $\widehat{KHC}$ = $90^0$ (gt)
Cạnh CH chung.
Do đó $\Delta$ AHC = $\Delta$ KHC (c-g-c)
Suy ra $\widehat{ACH}$ = $\widehat{KCH}$ (hai góc tương ứng)
Vậy CB là tia phân giác của góc ACK.
Ngoài ra còn có:
HA, HK là tia phân giác của góc bẹt BHC.
HB, HC là tia phân giác của góc bẹt AHK.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài 27 trang 119 sgk hình học 7 tập 1.
Nêu thêm một điều kiện để hai tam giác trong mỗi hình vẽ dưới đây là hai tam giác bằng nhau theo trường hợp cạnh - góc - cạnh:a) $\Delta$ ABC = $\Delta$ ADC (h.86).
b) $\Delta$ AMB = $\Delta$ EMC (h.87).
c) $\Delta$ CAB = $\Delta$ DBA (h.88).
Bài giải:
 |
| Hình 86 |
 |
| Hình 87. |
 |
| Hình 88. |
Giải bài 28 trang 120 sgk hình học 7 tập 1.
Trên hình 89 có các tam giác nào bằng nhau?Bài giải:
 |
| Hình 89. |
Xét tam giác DKE có $\widehat{D}$ + $\widehat{K}$ + $\widehat{E}$ = $180^0$ (theo định lí tổng ba góc của một tam giác)
Mà $\widehat{K}$ = $80^0$, $\widehat{E}$ = $40^0$ (gt)
Suy ra $\widehat{D}$ = $60^0$
Xét hai tam giác ABC và KDE có:
AB = KD (gt)
$\widehat{B}$ = $\widehat{D}$ = $60^0$
BC = DE (gt)
Suy ra $\Delta$ ABC = $\Delta$ KDE (c-g-c)
Còn $\Delta$ MNP không bằng hai tam giác còn lại vì không có đủ các điều kiện c-c-c hoặc c-g-c.
Giải bài 29 trang 120 sgk hình học 7 tập 1.
Cho góc xAy. Lấy điểm B trên tia Ax, điểm D trên tia Ay sao cho AB = AD. Trên tia Bx lấy điểm E, trên tia Dy lấy điểm C sao cho BE = DC. Chứng minh rằng $\Delta$ ABC = $\Delta$ ADE.Bài giải:
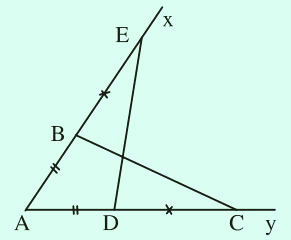 |
| AB = AD, BE = DC. |
Ta có $\left.\begin{matrix} AB = AD\\ BE = DC\end{matrix}\right\}$ => AE = AC.
Xét hai tam giác ABC và ADE có:
AB = AD (gt)
$\widehat{A}$ chung.
AC = AE (cmt)
Suy ra $\Delta$ ABC = $\Delta$ ADE (c-g-c)
Giải bài 30 trang 120 sgk hình học 7 tập 1.
Trên hình 90, các tam giác ABC và A'BC có cạnh chung BC = 3cm, CA = CA' = 2cm, $\widehat{ABC}$ = $\widehat{A'BC}$ = $30^0$ nhưng hai tam giác đó không bằng nhau. Tại sao ở đây không thể áp dụng trường hợp cạnh - góc - cạnh để kết luận $\Delta$ ABC = $\Delta$ A'BC?Bài giải:
 |
| Hình 90. |
$\widehat{ABC}$ không phải là góc xen giữa hai cạnh BC và CA
$\widehat{A'BC}$ không phải là góc xen giữa hai cạnh BC và CA'.
Nên không thể áp dụng trường hợp cạnh - góc - cạnh để kết luận $\Delta$ ABC = $\Delta$ A'BC
Giải bài 31 trang 120 sgk hình học 7 tập 1.
Cho đoạn thẳng AB, điểm M nằm trên đường trung trực của AB. So sánh độ dài các đoạn thẳng MA và MB.Bài giải:
Xét tam giác MIA và MIB có:
IA = IB (gt)
$\widehat{MIA}$ = $\widehat{MIB}$ = $90^0$ (gt)
Cạnh MI chung.
Nên $\Delta$ MIA = $\Delta$ MIB (c-g-c)
Suy ra MA = MB.
Giải bài 32 trang 120 sgk hình học 7 tập 1.
Tìm các tia phân giác trên hình 91. Hãy chứng minh điều đó.Bài giải:
 |
| Hình 91. |
AH = KH (gt)
$\widehat{AHB}$ = $\widehat{KHB}$ = $90^0$ (gt)
Cạnh BH chung.
Do đó $\Delta$ AHB = $\Delta$ KHB (c-g-c)
Suy ra $\widehat{ABH}$ = $\widehat{KBH}$ (hai góc tương ứng)
Vậy tia BC là tia phân giác của góc ABK.
Xét hai tam giác AHC và KHC có:
AH = KH (gt)
$\widehat{AHC}$ = $\widehat{KHC}$ = $90^0$ (gt)
Cạnh CH chung.
Do đó $\Delta$ AHC = $\Delta$ KHC (c-g-c)
Suy ra $\widehat{ACH}$ = $\widehat{KCH}$ (hai góc tương ứng)
Vậy CB là tia phân giác của góc ACK.
Ngoài ra còn có:
HA, HK là tia phân giác của góc bẹt BHC.
HB, HC là tia phân giác của góc bẹt AHK.
Xem bài trước: Giải bài tập trường hợp bằng nhau thứ hai cạnh góc cạnh
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon