Giải bài tập trường hợp bằng nhau thứ ba góc cạnh góc.
Việc xem xét hai tam giác có bằng nhau hay không ngày càng đơn giản khi ta có thêm trường hợp bằng nhau thứ ba góc cạnh góc.
Bài giải:
- Vẽ đoạn thẳng AC.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ tia Ax sao cho $\widehat{CAx}$ = $90^0$, vẽ tia Cy sao cho $\widehat{ACy}$ = $60^0$.
- Hai tia Ax và By cắt nhau tại B. Tam giác ABC là tam giác cần vẽ.
Bài giải:
Hình 98:
Xét hai tam giác BCA và BDA có:
$\left.\begin{matrix} \widehat{CBA} = \widehat{DBA} (gt)\\ Cạnh BA chung \\ \widehat{BAC} = \widehat{BAD} (gt) \end{matrix}\right\}$ => $\Delta$ BCA = $\Delta$ BDA (g-c-g)
Hình 99:
Ta có:
$\widehat{ABC}$ + $\widehat{ABD}$ = $180^0$ (hai góc kề bù)
=> $\widehat{ABD}$ = $180^0$ - $\widehat{ABC}$ (1)
$\widehat{ACB}$ + $\widehat{ACE}$ = $180^0$ (hai góc kề bù)
=> $\widehat{ACE}$ = $180^0$ - $\widehat{ACB}$ (2)
Mà $\widehat{ABC}$ = $\widehat{ACB}$ (3)
Từ (1), (2), (3) suy ra $\widehat{ABD}$ = $\widehat{ACE}$.
Xét hai tam giác ABD và ACE có:
$\left.\begin{matrix} \widehat{ADB} = \widehat{AEC} (gt)\\ DB = CE (gt) \\ \widehat{ABD} = \widehat{ACE} (cmt) \end{matrix}\right\}$ => $\Delta$ ABD = $\Delta$ ACE (g-c-g)
Ta có:
DC = DB + BC
EB = EC + BC
Mà DB = EC
Suy ra DC = EB
Xét hai tam giác ADC và AEB có:
$\left.\begin{matrix} \widehat{ADC} = \widehat{AEB} (gt)\\ DC = EB (cmt) \\ \widehat{ACD} = \widehat{ABE} (gt) \end{matrix}\right\}$ => $\Delta$ ADC = $\Delta$ AEB (g-c-g)
a) Chứng minh rằng OA = OB.
b) Lấy điểm C thuộc tia Ot, chứng minh rằng CA = CB và $\widehat{OAC}$ = $\widehat{OBC}$.
Bài giải:
a) Xét hai tam giác vuông HAO và HBO có:
$\widehat{O_1}$ = $\widehat{O_2}$ (vì Ot là tia phân giác của $\widehat{xOy}$)
Cạnh OH chung.
$\widehat{H_1}$ = $\widehat{H_2}$ = $90^0$
Vậy $\Delta$ HAO = $\Delta$ HBO (g-c-g)
Suy ra OA = OB (hai cạnh tương ứng)
b) Xét hai tam giác OAC và OBC có:
OA = OB (cmt)
$\widehat{O_1}$ = $\widehat{O_2}$
Cạnh OC chung.
Vậy $\Delta$ OAC = $\Delta$ OBC (c-g-c)
Suy ra CA = CB và $\widehat{OAC}$ = $\widehat{OBC}$ (đpcm)
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài 33 trang 123 sgk hình học 7 tập 1
Vẽ tam giác ABC biết AC = 2cm, $\widehat{A}$ = $90^0$, $\widehat{C}$ = $60^0$.Bài giải:
 |
| Vẽ tam giác ABC. |
- Vẽ đoạn thẳng AC.
- Trên cùng một nửa mặt phẳng bờ AC, vẽ tia Ax sao cho $\widehat{CAx}$ = $90^0$, vẽ tia Cy sao cho $\widehat{ACy}$ = $60^0$.
- Hai tia Ax và By cắt nhau tại B. Tam giác ABC là tam giác cần vẽ.
Giải bài 34 trang 123 sgk hình học 7 tập 1.
Trên mỗi hình 98, 99 có các tam giác nào bằng nhau? Vì sao?Bài giải:
Hình 98:
 |
| Hình 98. |
Xét hai tam giác BCA và BDA có:
$\left.\begin{matrix} \widehat{CBA} = \widehat{DBA} (gt)\\ Cạnh BA chung \\ \widehat{BAC} = \widehat{BAD} (gt) \end{matrix}\right\}$ => $\Delta$ BCA = $\Delta$ BDA (g-c-g)
Hình 99:
 |
| Hình 99. |
Ta có:
$\widehat{ABC}$ + $\widehat{ABD}$ = $180^0$ (hai góc kề bù)
=> $\widehat{ABD}$ = $180^0$ - $\widehat{ABC}$ (1)
$\widehat{ACB}$ + $\widehat{ACE}$ = $180^0$ (hai góc kề bù)
=> $\widehat{ACE}$ = $180^0$ - $\widehat{ACB}$ (2)
Mà $\widehat{ABC}$ = $\widehat{ACB}$ (3)
Từ (1), (2), (3) suy ra $\widehat{ABD}$ = $\widehat{ACE}$.
Xét hai tam giác ABD và ACE có:
$\left.\begin{matrix} \widehat{ADB} = \widehat{AEC} (gt)\\ DB = CE (gt) \\ \widehat{ABD} = \widehat{ACE} (cmt) \end{matrix}\right\}$ => $\Delta$ ABD = $\Delta$ ACE (g-c-g)
Ta có:
DC = DB + BC
EB = EC + BC
Mà DB = EC
Suy ra DC = EB
Xét hai tam giác ADC và AEB có:
$\left.\begin{matrix} \widehat{ADC} = \widehat{AEB} (gt)\\ DC = EB (cmt) \\ \widehat{ACD} = \widehat{ABE} (gt) \end{matrix}\right\}$ => $\Delta$ ADC = $\Delta$ AEB (g-c-g)
Giải bài 35 trang 123 sgk hình học 7 tập 1.
Cho góc xOy khác góc bẹt, Ot là tia phân giác của góc đó. Qua điểm H thuộc tia Ot, kẻ đường vuông góc với Ot, nó cắt Ox và Oy theo thứ tự ở A và B.a) Chứng minh rằng OA = OB.
b) Lấy điểm C thuộc tia Ot, chứng minh rằng CA = CB và $\widehat{OAC}$ = $\widehat{OBC}$.
Bài giải:
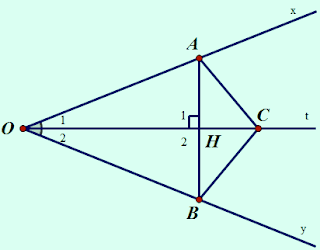 |
| Ot là tia phân giác góc xOy. |
a) Xét hai tam giác vuông HAO và HBO có:
$\widehat{O_1}$ = $\widehat{O_2}$ (vì Ot là tia phân giác của $\widehat{xOy}$)
Cạnh OH chung.
$\widehat{H_1}$ = $\widehat{H_2}$ = $90^0$
Vậy $\Delta$ HAO = $\Delta$ HBO (g-c-g)
Suy ra OA = OB (hai cạnh tương ứng)
b) Xét hai tam giác OAC và OBC có:
OA = OB (cmt)
$\widehat{O_1}$ = $\widehat{O_2}$
Cạnh OC chung.
Vậy $\Delta$ OAC = $\Delta$ OBC (c-g-c)
Suy ra CA = CB và $\widehat{OAC}$ = $\widehat{OBC}$ (đpcm)
Xem bài trước: Giải bài luyện tập trường hợp bằng nhau cạnh góc cạnh.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon