Giải bài tập về đa giác.
Giải bài 1 trang 115 sgk hình học 8 tập 1
Hãy vẽ phác một lục giác lồi. Hãy nêu cách nhận biết một đa giác lồi.Bài giải:
Ta có thể vẽ như sau:
 |
| Lục giác lồi. |
Giải bài 2 trang 115 sgk hình học 8 tập 1
Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:a) Có tất cả các cạnh bằng nhau
b) Có tất cả các góc bằng nhau.
Bài giải:
a) Ta có một dạng hình học đã được học có bốn cạnh bằng nhau, đó là hình thoi, tuy nhiên các góc của hình thoi lại không bằng nhau. Nên có thể nói hình thoi là một tứ giác không đều.
b) Có bốn góc bằng nhau, ta cũng đã biết, đó là hình chữ nhật. Nhưng các cạnh của hình chữ nhật không bằng nhau. Nên hình chữ nhật chính là một đa giác không đều có các góc bằng nhau.
Giải bài 3 trang 115 sgk hình học 8 tập 1
Cho hình thoi ABCD có góc $\widehat{A}$ = $60^0$. Gọi EFGH lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.Bài giải:
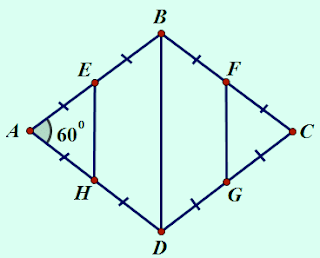 |
| Chứng minh EBFGDH là lục giác đều. |
Ta có AB = BC = CD = DA (vì ABCD là hình thoi)
=> EB = BF = GD = DH (1)
Ta có AB = AD nên tam giác ABD cân tại A
có $\widehat{A}$ = $60^0$
Do đó tam giác HAE đều.
=> AB = BD = DA
Ta lại có EH, FG là đường trung bình của tam giác ABD và CBD.
Nên EH = FG = $\frac{BD}{2}$
<=> EH = FG = $\frac{AB}{2}$ (vì AB = BD cmt)
<=> EH = FG = EB (2)
Từ (1) và (2) suy ra EB = BF = FG = GD = DH = HE (3)
Ta có $\widehat{EBF}$ = $\widehat{HDG}$ = $120^0$ (cùng bù với góc A)
Ta lại có các tam giác ABD, CBD, AEH, CFG là những tam giác đều.
Nên $\widehat{HEB}$ = $\widehat{BFG}$ = $\widehat{FGD}$ = $\widehat{DHE}$ = $120^0$
Suy ra $\widehat{EBF}$ = $\widehat{HDG}$ = $\widehat{HEB}$ = $\widehat{BFG}$ = $\widehat{FGD}$ = $\widehat{DHE}$ = $120^0$
Vậy tứ giác EBFGDH có 6 góc bằng nhau (4)
Từ (3) và (4) suy ra tứ giác EBFGDH là lục giác đều (đpcm)
Giải bài 4 trang 115 sgk hình học 8 tập 1
Điền số thích hợp vào ô trống trong bảng sau:Bài giải:
Ta điền như sau:
|
|
|
|
|
Đa
giác n cạnh
|
|
Số
cạnh
|
4
|
5
|
6
|
n
|
|
Số
đường chéo xuất phát từ 1 đỉnh
|
1
|
2
|
3
|
n
- 3
|
|
Số
tam giác được tạo thành.
|
2
|
3
|
4
|
n
- 2
|
|
Tổng
số đo các góc của đa giác.
|
2.
.$180^0$ = .$360^0$
|
3.
.$180^0$ = .$540^0$
|
4.$180^0$
= $720^0$
|
(n
– 2). .$180^0$
|
Giải bài 5 trang 115 sgk hình học 8 tập 1
Tính số đo mỗi góc của ngũ giác đều, lục giác đều, n-giác đều.Bài giải:
Ta đã biết hình n-giác đều có n góc ở n đỉnh và dĩ nhiên các góc này bằng nhau.
Tổng số đo các góc của đa giác đều n cạnh bằng (n - 2).$180^0$
Do đó số đo của mỗi góc tại đỉnh là $\frac{(n - 2).180^0}{n}$
+ Với hình ngũ giác đều ta có n = 5 nên số đo góc tại mỗi đỉnh là $\frac{(5 - 2).180^0}{5}$ = $108^0$
+ Với hình lục giác đều, ta có n = 6 nên số đo góc tại mỗi đỉnh là $\frac{(6 - 2).180^0}{6}$ = $120^0$
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon