Giải bài tập hình vuông.
Định nghĩa, tính chất, dấu hiệu nhận biết hình bình hành, hình chữ nhật, hình thoi, hình vuông, một lần nữa sẽ được củng cố thông qua việc hoàn thành các bài tập về hình vuông ngay sau đây.
b) Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng: 1dm, $\frac{3}{2}$dm, $\sqrt{2}$dm hay $\frac{4}{3}$dm?
Bài giải:
a) Áp dụng định lí Pi-ta-go trong hình vuông ABC, ta có:
$AC^2$ = $AB^2$ + $BC^2$ = $3^2$ + $3^2$ = 18
=> AC = $\sqrt{18}$
Vậy đường chéo của hình vuông bằng $\sqrt{18}$cm.
b) Tương tự, cũng áp dụng định lí Pi-ta-go vào tam giác vuông ABC, nhưng bài này cho độ dài đường chéo, tức AC = 2dm, tính cạnh AB.
Ta có: $AC^2$ = $AB^2$ + $BC^2$ = 2$AB^2$ (vì AB = BC)
=> $AB^2$ = $\frac{AC^2}{2}$ = $\frac{2^2}{2}$ = 2
=> AB = $\sqrt{2}$
Vậy cạnh hình vuông bằng $\sqrt{2}$dm.
Bài giải:
- Tâm đối xứng của hình vuông chính là giao điểm hai đường chéo (vì hình thoi là hình bình hành đặc biệt mà hình vuông cũng là một trường hợp đặc biệt của hình thoi)
- Hình vuông là hình thoi, cũng là hình chữ nhật nên hai đường chéo và hai đường thẳng đi qua trung điểm các cặp cạnh đối là trục đối xứng của hình vuông.
Bài giải:
Tứ giác AEDF có $\widehat{A}$ = $\widehat{E}$ = $\widehat{F}$ = $90^0$ nên AEDF là hình chữ nhật.
Mặt khác $\widehat{EAD}$ = $\widehat{DAF}$ = $45^0$
Suy ra AD là đường phân giác của góc A.
Hình chữ nhật AEDF có AD là đường phân giác của góc A nên AEDF là hình vuông.
Bài giải:
Xét $\Delta$ AEH, $\Delta$ BFE, $\Delta$ CGF, $\Delta$ DHG có:
AE = BF = CG = DH (gt) (1)
$\widehat{A}$ = $\widehat{B}$ = $\widehat{C}$ = $\widehat{D}$ = $90^0$ (vì ABCD là hình vuông) (2)
Mặt khác ta có:
AH = AD - DH
BE = AB - AE
CF = CB - BF
DG = DC - GC
Mà AB = BC = CD = AD (vì ABCD là hình vuông)
Nên AH = BE = CF = DG (3)
Từ (1), (2), (3) suy ra $\Delta$ AEH = $\Delta$ BFE = $\Delta$ CGF = $\Delta$ DHG (c-g-c)
Suy ra HE = FE = FG = GH (cạnh tương ứng)
Do đó EFGH là hình thoi. (*)
Ta lại có: $\widehat{H_3}$ = $\widehat{E_3}$ (vì $\Delta$ AEH = $\Delta$ BFE)
Mà $\widehat{H_3}$ + $\widehat{E_1}$ = $90^0$ (hai góc phụ nhau)
Hay $\widehat{E_3}$ + $\widehat{E_1}$ = $90^0$
Suy ra $\widehat{E_2}$ = $90^0$ (**)
Từ (*) và (**) suy ra EFGH là hình vuông (theo dấu hiệu 4)
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài tập 79 trang 108 sgk hình học 8 tập 1.
a) Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng: 6cm, $\sqrt{18}$cm, 5cm, hay 4cm?b) Đường chéo của một hình vuông bằng 2dm. Cạnh của hình vuông đó bằng: 1dm, $\frac{3}{2}$dm, $\sqrt{2}$dm hay $\frac{4}{3}$dm?
Bài giải:
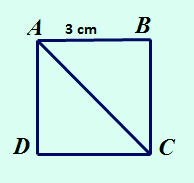 |
| Hình vuông cạnh 3cm. |
a) Áp dụng định lí Pi-ta-go trong hình vuông ABC, ta có:
$AC^2$ = $AB^2$ + $BC^2$ = $3^2$ + $3^2$ = 18
=> AC = $\sqrt{18}$
Vậy đường chéo của hình vuông bằng $\sqrt{18}$cm.
b) Tương tự, cũng áp dụng định lí Pi-ta-go vào tam giác vuông ABC, nhưng bài này cho độ dài đường chéo, tức AC = 2dm, tính cạnh AB.
Ta có: $AC^2$ = $AB^2$ + $BC^2$ = 2$AB^2$ (vì AB = BC)
=> $AB^2$ = $\frac{AC^2}{2}$ = $\frac{2^2}{2}$ = 2
=> AB = $\sqrt{2}$
Vậy cạnh hình vuông bằng $\sqrt{2}$dm.
Giải bài tập 80 trang 108 sgk hình học 8 tập 1.
Hãy chỉ rõ tâm đối xứng của hình vuông, các trục đối xứng của hình vuông.Bài giải:
- Tâm đối xứng của hình vuông chính là giao điểm hai đường chéo (vì hình thoi là hình bình hành đặc biệt mà hình vuông cũng là một trường hợp đặc biệt của hình thoi)
- Hình vuông là hình thoi, cũng là hình chữ nhật nên hai đường chéo và hai đường thẳng đi qua trung điểm các cặp cạnh đối là trục đối xứng của hình vuông.
Giải bài tập 81 trang 108 sgk hình học 8 tập 1.
Cho hình 106. Tứ giác AEDF là hình gì? Vì sao?Bài giải:
 |
| Hình 106 |
Mặt khác $\widehat{EAD}$ = $\widehat{DAF}$ = $45^0$
Suy ra AD là đường phân giác của góc A.
Hình chữ nhật AEDF có AD là đường phân giác của góc A nên AEDF là hình vuông.
Giải bài tập 82 trang 108 sgk hình học 8 tập 1.
Cho hình 107, trong đó ABCD là hình vuông. Chứng minh rằng tứ giác EFGH là hình vuông.Bài giải:
 |
| Hình 107. |
AE = BF = CG = DH (gt) (1)
$\widehat{A}$ = $\widehat{B}$ = $\widehat{C}$ = $\widehat{D}$ = $90^0$ (vì ABCD là hình vuông) (2)
Mặt khác ta có:
AH = AD - DH
BE = AB - AE
CF = CB - BF
DG = DC - GC
Mà AB = BC = CD = AD (vì ABCD là hình vuông)
Nên AH = BE = CF = DG (3)
Từ (1), (2), (3) suy ra $\Delta$ AEH = $\Delta$ BFE = $\Delta$ CGF = $\Delta$ DHG (c-g-c)
Suy ra HE = FE = FG = GH (cạnh tương ứng)
Do đó EFGH là hình thoi. (*)
Ta lại có: $\widehat{H_3}$ = $\widehat{E_3}$ (vì $\Delta$ AEH = $\Delta$ BFE)
Mà $\widehat{H_3}$ + $\widehat{E_1}$ = $90^0$ (hai góc phụ nhau)
Hay $\widehat{E_3}$ + $\widehat{E_1}$ = $90^0$
Suy ra $\widehat{E_2}$ = $90^0$ (**)
Từ (*) và (**) suy ra EFGH là hình vuông (theo dấu hiệu 4)
Xem bài trước: Giải bài tập về hình thoi.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon