Giải bài luyện tập về ba trường hợp bằng nhau của tam giác.
Khi học về hai tam giác bằng nhau, ta có ba trường hợp bằng nhau của tam giác. Trường hợp thứ nhất là cạnh cạnh cạnh, trường hợp thứ hai là cạnh góc cạnh và trường hợp thứ ba là góc cạnh góc. Hôm nay, ta cùng luyện tập về ba trường hợp bằng nhau của tam giác để có được sự linh hoạt khi áp dụng từng trường hợp bằng nhau trong việc giải quyết các bài tập toán có liên quan.
a) AD = BC
b) $\Delta$ EAB = $\Delta$ ECD.
c) OE là tia phân giác của góc xOy.
Bài giải:
a) Chứng minh AD = BC.
Xét hai tam giác AOD và COB có:
OA = OC (gt)
$\widehat{O}$ chung.
OB = OD (gt)
Vậy $\Delta$ AOD = $\Delta$ COB (c-g-c)
Suy ra AD = BC (hai cạnh tương ứng)
b) Chứng minh $\Delta$ EAB = $\Delta$ ECD.
Ta có:
$\Delta$ AOD = $\Delta$ COB (cmt)
Suy ra $\widehat{A_2}$ = $\widehat{C_2}$ và $\widehat{D}$ = $\widehat{B}$.
Vì $\widehat{A_1}$ và $\widehat{A_2}$ là hai góc kề bù nên:
$\widehat{A_1}$ = $180^0$ - $\widehat{A_2}$
Hay $\widehat{A_1}$ = $180^0$ - $\widehat{C_2}$ ($\widehat{A_2}$ = $\widehat{C_2}$ cmt)
Mà $180^0$ - $\widehat{C_2}$ = $\widehat{C_1}$ (hai góc kề bù)
Suy ra $\widehat{A_1}$ = $\widehat{C_1}$
Ta lại có AB = OB - OA
CD = OD - OC
Mà OA = OC, OB = OD (gt)
Nên AB = CD.
Khi đó hai tam giác EAB và ECD có:
$\left.\begin{matrix} \widehat{D} = \widehat{B}\\ AB = CD \\ \widehat{A_1} = \widehat{C_1} \end{matrix}\right\}$ (cmt)
Suy ra $\Delta$ EAB = $\Delta$ ECD (g-c-g).
c) Chứng minh OE là tia phân giác của góc xOy.
Xét hai tam giác AOE và COE có:
EA = EC (vì $\Delta$ EAB = $\Delta$ ECD)
OA = OC (gt)
Cạnh OE chung.
Vậy $\Delta$ AOE = $\Delta$ COE (c-c-c)
Suy ra $\widehat{AOE}$ = $\widehat{COE}$.
Nói cách khác OE là tia phân giác góc AOC
Hay OE là tia phân giác góc xOy.
a) $\Delta$ ADB = $\Delta$ ADC.
b) AB = AC.
Bài giải:
a) Chứng minh $\Delta$ ADB = $\Delta$ ADC.
Ta có: $\widehat{A_1}$ + $\widehat{B}$ + $\widehat{D_1}$ = $180^0$
=> $\widehat{D_1}$ = $180^0$ - ($\widehat{A_1}$ + $\widehat{B}$)
Mà $\widehat{A_1}$ = $\widehat{A_2}$ (vì AD là tia phân giác góc A)
Và $\widehat{B}$ = $\widehat{C}$ (gt)
Nên $\widehat{D_1}$ = $180^0$ - ($\widehat{A_2}$ + $\widehat{C}$)
Mà $180^0$ - ($\widehat{A_2}$ + $\widehat{C}$) = $\widehat{D_2}$
Do đó $\widehat{D_1}$ = $\widehat{D_2}$.
Xét hai tam giác ADB và ADC có:
$\widehat{A_1}$ = $\widehat{A_2}$ (vì AD là tia phân giác góc A)
Cạnh AD chung
$\widehat{D_1}$ = $\widehat{D_2}$. (cmt)
Vậy $\Delta$ ADB = $\Delta$ ADC (g-c-g)
b) Chứng minh AB = AC.
Ta có $\Delta$ ADB = $\Delta$ ADC (cmt)
Suy ra AB = AC (hai cạnh tương ứng).
a) AB = CD, BC = AD
b) AB // CD.
Bài giải:
a) Chứng minh:
➤ AB = CD.
Xét hai tam giác EAB và FCD có:
EB = FD (bằng 1 ô vuông)
$\widehat{AEB}$ = $\widehat{CFD}$.
EA = FC (bằng 3 ô vuông)
Vậy $\Delta$ EAB = $\Delta$ FCD
Suy ra AB = CD (hai cạnh tương ứng)
➤ BC = AD.
Xét hai tam giác GBC và HDA có:
KB = PD (bằng 2 ô vuông)
$\widehat{CKB}$ = $\widehat{AHD}$.
GC = AH (bằng 5 ô vuông)
Vậy $\Delta$ GBC = $\Delta$ HDA.
Suy ra BC = AD. (hai cạnh tương ứng)
b) Chứng minh AB // CD.
Xét hai tam giác BAD và DCB có:
AB = CD (cmt)
Cạnh BD chung.
BC = AD (cmt)
Vậy $\Delta$ BAD = $\Delta$ DCB (c-c-c)
Suy ra $\left.\begin{matrix} \widehat{B_1} = \widehat{D_1}\\ Mà \, \widehat{B_1} \, và \, \widehat{D_1} \,ở \, vị \, trí \, so\, le\, trong\end{matrix}\right\}$ => AB //CD.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Giải bài 43 trang 125 sgk hình học 7 tập 1.
Cho góc xOy khác góc bẹt. Lấy các điểm A, B thuộc tia Ox sao cho OA < OB. Lấy các điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi F là giao điểm của AD và BC. Chứng minh rằng:a) AD = BC
b) $\Delta$ EAB = $\Delta$ ECD.
c) OE là tia phân giác của góc xOy.
Bài giải:
a) Chứng minh AD = BC.
Xét hai tam giác AOD và COB có:
OA = OC (gt)
$\widehat{O}$ chung.
OB = OD (gt)
Vậy $\Delta$ AOD = $\Delta$ COB (c-g-c)
Suy ra AD = BC (hai cạnh tương ứng)
b) Chứng minh $\Delta$ EAB = $\Delta$ ECD.
 |
| Góc xOy khác góc bẹt. |
$\Delta$ AOD = $\Delta$ COB (cmt)
Suy ra $\widehat{A_2}$ = $\widehat{C_2}$ và $\widehat{D}$ = $\widehat{B}$.
Vì $\widehat{A_1}$ và $\widehat{A_2}$ là hai góc kề bù nên:
$\widehat{A_1}$ = $180^0$ - $\widehat{A_2}$
Hay $\widehat{A_1}$ = $180^0$ - $\widehat{C_2}$ ($\widehat{A_2}$ = $\widehat{C_2}$ cmt)
Mà $180^0$ - $\widehat{C_2}$ = $\widehat{C_1}$ (hai góc kề bù)
Suy ra $\widehat{A_1}$ = $\widehat{C_1}$
Ta lại có AB = OB - OA
CD = OD - OC
Mà OA = OC, OB = OD (gt)
Nên AB = CD.
Khi đó hai tam giác EAB và ECD có:
$\left.\begin{matrix} \widehat{D} = \widehat{B}\\ AB = CD \\ \widehat{A_1} = \widehat{C_1} \end{matrix}\right\}$ (cmt)
Suy ra $\Delta$ EAB = $\Delta$ ECD (g-c-g).
c) Chứng minh OE là tia phân giác của góc xOy.
Xét hai tam giác AOE và COE có:
EA = EC (vì $\Delta$ EAB = $\Delta$ ECD)
OA = OC (gt)
Cạnh OE chung.
Vậy $\Delta$ AOE = $\Delta$ COE (c-c-c)
Suy ra $\widehat{AOE}$ = $\widehat{COE}$.
Nói cách khác OE là tia phân giác góc AOC
Hay OE là tia phân giác góc xOy.
Giải bài 44 trang 125 sgk hình học 7 tập 1.
Cho tam giác ABC có $\widehat{B}$ = $\widehat{C}$. Tia phân giác của góc A cắt BC tại D. Chứng minh rằng:a) $\Delta$ ADB = $\Delta$ ADC.
b) AB = AC.
Bài giải:
a) Chứng minh $\Delta$ ADB = $\Delta$ ADC.
Ta có: $\widehat{A_1}$ + $\widehat{B}$ + $\widehat{D_1}$ = $180^0$
=> $\widehat{D_1}$ = $180^0$ - ($\widehat{A_1}$ + $\widehat{B}$)
Mà $\widehat{A_1}$ = $\widehat{A_2}$ (vì AD là tia phân giác góc A)
Và $\widehat{B}$ = $\widehat{C}$ (gt)
Nên $\widehat{D_1}$ = $180^0$ - ($\widehat{A_2}$ + $\widehat{C}$)
Mà $180^0$ - ($\widehat{A_2}$ + $\widehat{C}$) = $\widehat{D_2}$
Do đó $\widehat{D_1}$ = $\widehat{D_2}$.
Xét hai tam giác ADB và ADC có:
$\widehat{A_1}$ = $\widehat{A_2}$ (vì AD là tia phân giác góc A)
Cạnh AD chung
$\widehat{D_1}$ = $\widehat{D_2}$. (cmt)
Vậy $\Delta$ ADB = $\Delta$ ADC (g-c-g)
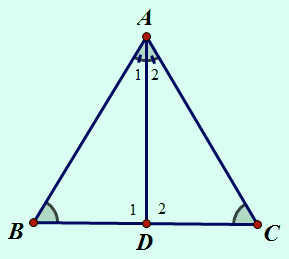 |
| AD là tia phân giác góc D. |
Ta có $\Delta$ ADB = $\Delta$ ADC (cmt)
Suy ra AB = AC (hai cạnh tương ứng).
Giải bài 45 trang 125 sgk hình học 7 tập 1.
Đố: Cho bốn đoạn thẳng AB, BC, CD, DA trên giấy kẻ ô vuông như ở hình 110. Hãy dùng lập luận để giải thích:a) AB = CD, BC = AD
b) AB // CD.
Bài giải:
a) Chứng minh:
➤ AB = CD.
Xét hai tam giác EAB và FCD có:
EB = FD (bằng 1 ô vuông)
$\widehat{AEB}$ = $\widehat{CFD}$.
EA = FC (bằng 3 ô vuông)
Vậy $\Delta$ EAB = $\Delta$ FCD
Suy ra AB = CD (hai cạnh tương ứng)
➤ BC = AD.
Xét hai tam giác GBC và HDA có:
KB = PD (bằng 2 ô vuông)
$\widehat{CKB}$ = $\widehat{AHD}$.
GC = AH (bằng 5 ô vuông)
Vậy $\Delta$ GBC = $\Delta$ HDA.
Suy ra BC = AD. (hai cạnh tương ứng)
 |
| Hình 110. Chứng minh AB // CD. |
Xét hai tam giác BAD và DCB có:
AB = CD (cmt)
Cạnh BD chung.
BC = AD (cmt)
Vậy $\Delta$ BAD = $\Delta$ DCB (c-c-c)
Suy ra $\left.\begin{matrix} \widehat{B_1} = \widehat{D_1}\\ Mà \, \widehat{B_1} \, và \, \widehat{D_1} \,ở \, vị \, trí \, so\, le\, trong\end{matrix}\right\}$ => AB //CD.
Xem bài trước: Luyện tập trường hợp bằng nhau cạnh góc cạnh.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

EmoticonEmoticon