Tia

Bắt đầu từ một điểm, đến nay, các bạn lớp 6 đã đi qua được một đường thẳng với những trãi nghiệm đầy thú vị. Và nếu tiếp tục cuộc hành trình, ta sẽ gặp tia. Ở đó, có rất nhiều điều hấp dẫn đang chờ ta khám phá.

Thế nào là tia?

Vẽ đường thẳng xy, việc này bạn nào cũng thực hiện được. Sau đó, lấy điểm O trên đường thẳng xy.

Hai tia gốc O.

Quan sát hình vẽ, ta thấy điểm O chia đường thẳng xy thành 2 phần: phần màu đỏ gồm điểm O và đường thẳng màu đỏ, phần màu xanh gồm điểm O và đường thẳng màu xanh. Mỗi phần màu đỏ và phần màu xanh đó được gọi là một tia gốc O.
Ta có định nghĩa về tia như sau:

Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O.

Với hình vẽ trên, phần màu đỏ gọi là tia Ox, phần màu xanh là tia Oy.
Tia Ox còn gọi là nửa đường thẳng Ox, bị giới hạn bởi điểm O, không bị giới hạn về phía x.
Tia Oy còn gọi là nửa đường thẳng Oy, bị giới hạn bởi điểm O, không bị giới hạn về phía y.
Lưu ý: Khi đọc (hay viết) tên một tia, phải đọc (hay viết) tên gốc trước.

Hai tia đối nhau.

Quan sát hình 2, ta thấy có 3 tia: Ox, Oy và Oz. Trong đó hai tia Ox, Oy tạo thành đường thẳng xy, ta nói hai tia Ox, Oy đối nhau.

Hình 2. Hai tia đối nhau.

Hai tia đối nhau được định nghĩa như sau:

Hai tia chung gốc Ox và Oy tạo thành đường thẳng xy gọi là hai tia đối nhau.

Như vậy, hai tia đối nhau phải thỏa mãn đồng thời hai điều kiện:
- chúng có chung gốc
- cùng tạo thành một đường thẳng.
Cũng trên hình 2, ta lấy điểm M nằm trên tia Oy. Lúc này xuất hiện thêm các tia My, Mx, MO, OM. Trong đó hai tia Mx và My là hai tia đối nhau. Ta rút ra nhận xét mỗi điểm trên đường thẳng là gốc chung của hai tia đối nhau.

Hai tia trùng nhau

Quan sát hình 3, ta thấy có hai tia chung gốc A, đó là tia AB màu đỏ nằm trên tia Ax màu xanh. Khi đó hai tia AB và Ax trùng nhau.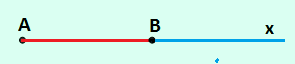

Hình 3, Hai tia trùng nhau.

Hai tia trùng nhau là hai tia mà mọi điểm đều là điểm chung.

Lưu ý:
- Hai tia không trùng nhau là hai tia phân biệt.
- Khi nói hai tia mà không nói gì thêm, ta hiểu đó là hai tia phân biệt.

Đến đây, các bạn đã có những hiểu biết cơ bản về tia, đã phân biệt được hai tia đối nhau, hai tia trùng nhau. Có một sự kết nối rõ ràng hơn giữa những điều đã học về điểm và đường thẳng với tia. Dù đã hiểu, đã nhớ, nhưng không được quên việc giải bài tập, chỉ có giải bài tập thì những kiến thức cô giáo đã dạy mới còn lại mãi với chúng ta.

Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!

CÙNG CHIA SẺ ĐỂ KIẾN THỨC ĐƯỢC LAN TỎA!

Be a Fan

Bài học liên quan.