Giải bài tập góc ở tâm.
Giải bài 1 trang 68 sgk hình học 9 tập 2.
Kim giờ và kim phút của đồng hồ tạo thành một góc ở tâm có số đo là bao nhiêu độ vào những thời điểm sau:a) 3 giờ b) 5 giờ c) 6 giờ d) 12 giờ e) 20 giờ.
Bài giải:
 |
| Góc ở tâm là bao nhiêu? |
Ta biết trên mặt đồng hồ chia thành 12 phần bằng nhau, nên mỗi phần sẽ có số đo là:
$360^0$ : 12 = $30^0$.
a) Lúc 3 giờ, kim dài và kim phút tạo thành góc ở tâm có số đo bằng $30^0$.3 = $90^0$
b) Lúc 5 giờ, kim dài và kim phút tạo thành góc ở tâm có số đo bằng $30^0$.5 = $150^0$
c) Lúc 6 giờ, kim dài và kim phút tạo thành góc ở tâm có số đo bằng $30^0$.6 = $180^0$
d) Lúc 12 giờ, kim dài và kim phút tạo thành góc ở tâm có số đo bằng $0^0$.
e) Lúc 20 giờ (8 giờ tối), kim dài và kim phút tạo thành góc ở tâm có số đo bằng $30^0$.4 = $120^0$.
Lưu ý: Ta không nên nhầm lẫn góc ở tâm lúc 20 giờ là $240^0$ vì số đo góc luôn nhỏ hơn hoặc bằng $180^0$.
Giải bài 2 trang 69 sgk hình học 9 tập 2.
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc $40^0$. Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.Bài giải:
 |
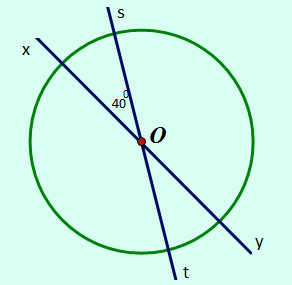| Tính số đo các góc ở tâm. |
Hai đường thẳng xy và st cắt nhau tại O, tạo thành 6 góc ở tâm, đó là:
$\widehat{xOs}$, $\widehat{sOy}$, $\widehat{yOt}$, $\widehat{tOx}$, $\widehat{xOy}$, $\widehat{sOt}$.
Ta có:
$\widehat{xOs}$ = $\widehat{yOt}$ = $40^0$ (hai góc đối đỉnh).
$\widehat{xOs}$ + $\widehat{sOy}$ = $180^0$ (hai góc kề bù)
=> $\widehat{sOy}$ = $180^0$ - $\widehat{xOs}$ = $180^0$ - $40^0$ = $140^0$
Suy ra $\widehat{tOx}$ = $\widehat{sOy}$ = $140^0$ (hai góc đối đỉnh)
$\widehat{xOy}$ = $\widehat{sOt}$ = $180^0$ (góc bẹt)
Giải bài 3 trang 69 sgk hình học 9 tập 2.
Trên các hình 5, 6 hãy dùng dụng cụ đo góc để tìm số đo cung AmB. Từ đó, tính số đo cung AnB tương ứng.Bài giải:
- Hình 5: Dùng thước đo góc, ta đo được góc nhỏ $\widehat{AOB}$ có số đo bằng $124^0$.
Do đó sđ cung AmB = $\widehat{AOB}$ = $124^0$
Suy ra sđ cung AnB = $360^0$ - $124^0$ = $236^0$
- Hình 6: Dùng thước đo góc, ta đo được góc nhỏ $\widehat{AOB}$ có số đo bằng $67^0$.
Do đó sđ cung AmB = $\widehat{AOB}$ = $67^0$
Suy ra sđ cung AnB = $360^0$ - $67^0$ = $293^0$
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
EmoticonEmoticon