Giải bài luyện tập về tiên đề Ơ-clit.
Trước khi giải bài luyện tập về tiên đề Ơ-clit, ta cần chuẩn bị một chút về mặt kiến thức và kỹ năng:
Bài giải:
Theo tiên đề Ơ-clit qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó. Do đó:
- Qua đỉnh A, ta vẽ được một đường thẳng a duy nhất song song với BC
- Qua đỉnh B, ta vẽ được duy nhất một đường thẳng b song song với AC
a) $\widehat{A_1}$ = ... (vì là cặp góc so le trong)
b) $\widehat{A_2}$ = ... (vì là cặp góc đồng vị)
c) $\widehat{B_3}$ + $\widehat{A_4}$ = ... (vì ... )
d) $\widehat{B_4}$ = $\widehat{A_2}$ (vì ... )
Bài giải:
a) $\widehat{A_1}$ = $\widehat{B_3}$ (vì là cặp góc so le trong)
b) $\widehat{A_2}$ = $\widehat{B_2}$ (vì là cặp góc đồng vị)
c) $\widehat{B_3}$ + $\widehat{A_4}$ = $180^0$ (vì là hai góc trong cùng phía)
d) $\widehat{B_4}$ = $\widehat{A_2}$ (vì cùng bằng $\widehat{B_2}$ )
Bài giải:
Hình 25a
- Biết d // d' thì suy ra:
a) $\widehat{A_1}$ = $\widehat{B_3}$ b) ... c) ...
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) ...
b) ...
c) ...
Hình 25b
- Biết:
a) $\widehat{A_4}$ = $\widehat{B_2}$ hoặc b) ... hoặc c) ...
thì suy ra d // d'
- Nếu một đường thẳng cắt hai đường thẳng mà a) ... hoặc b) ... hoặc c) ... thì hai đường thẳng đó song song với nhau.
Bài giải:
Hình 25a
- Biết d // d' thì suy ra:
a) $\widehat{A_1}$ = $\widehat{B_3}$
b) $\widehat{A_2}$ = $\widehat{B_2}$
c) $\widehat{A_1}$ + $\widehat{B_2}$ = $180^0$
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau
b) Hai góc đồng vị bằng nhau
c) Hai góc trong cùng phía bù nhau
Hình 25b
- Biết:
a) $\widehat{A_4}$ = $\widehat{B_2}$
hoặc b) $\widehat{A_3}$ = $\widehat{B_3}$
hoặc c) $\widehat{A_4}$ + $\widehat{B_3}$ = $180^0$
thì suy ra d // d'
- Nếu một đường thẳng cắt hai đường thẳng mà
a) Hai góc so le trong bằng nhau
hoặc b) Hai góc đồng vị bằng nhau
hoặc c) Hai góc trong cùng phía bù nhau
thì hai đường thẳng đó song song với nhau.
Tính góc nhọn tạo bởi a và $d_2$
Gợi ý: Tính số đo của một góc nhọn đỉnh A.
Bài giải:
Kéo dài đường thẳng a cắt $d_2$ tại B. Khi đó đường thẳng a tạo với $d_2$ một góc nhọn $\widehat{B_1}$
Ta có $A_1$ và $A_2$ là hai góc kề bù nên:
$A_1$ + $A_2$ = $180^0$
<=> $A_1$ + $150^0$ = $180^0$
<=> $A_1$ = $180^0$ - $150^0$ = $30^0$
Ta cũng có:
$\left.\begin{matrix} d_1 // d_2\\ \widehat{A_1}\, và\, \widehat{B_1} so\,le\,trong\end{matrix}\right\}$ => $\widehat{A_1}$ = $\widehat{B_1}$ = $30^0$
Vậy góc nhọn tạo bởi a và $d_2$ là $\widehat{B_1}$ = $30^0$
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
- Với hai đường thẳng song song và một cát tuyến, khi cho số đo của một góc, ta biết cách tính các góc còn lại.
- Vận dụng tiên đề Ơ clit và tính chất của hai đường thẳng song song để giải quyết yêu cầu của bài toán.
Giải bài 35 trang 94 sgk hình học 7 tập 1
Cho tam giác ABC. Qua đỉnh A vẽ đường thẳng a song song với BC, qua đỉnh B vẽ đường thẳng b song song với AC. Hỏi vẽ được mấy đường thẳng a, mấy đường thẳng b, vì sao?Bài giải:
Theo tiên đề Ơ-clit qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó. Do đó:
- Qua đỉnh A, ta vẽ được một đường thẳng a duy nhất song song với BC
- Qua đỉnh B, ta vẽ được duy nhất một đường thẳng b song song với AC
Giải bài 36 trang 94 sgk hình học 7 tập 1
Hình 23 cho biết a // b và c cắt a tại A, cắt b tại B. Hãy điền vào chỗ trống (...) trong các câu sau:a) $\widehat{A_1}$ = ... (vì là cặp góc so le trong)
b) $\widehat{A_2}$ = ... (vì là cặp góc đồng vị)
c) $\widehat{B_3}$ + $\widehat{A_4}$ = ... (vì ... )
d) $\widehat{B_4}$ = $\widehat{A_2}$ (vì ... )
Bài giải:
 |
| Hình 23 |
a) $\widehat{A_1}$ = $\widehat{B_3}$ (vì là cặp góc so le trong)
b) $\widehat{A_2}$ = $\widehat{B_2}$ (vì là cặp góc đồng vị)
c) $\widehat{B_3}$ + $\widehat{A_4}$ = $180^0$ (vì là hai góc trong cùng phía)
d) $\widehat{B_4}$ = $\widehat{A_2}$ (vì cùng bằng $\widehat{B_2}$ )
Giải bài 37 trang 95 sgk hình học 7 tập 1
Cho hình 24 (a // b). Hãy nêu tên các cặp góc bằng nhau của hai tam giác CAB và CDE.Bài giải:
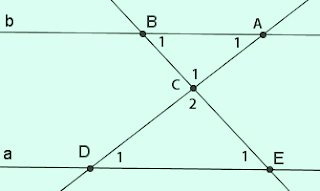 |
| Hình 24 |
Ta có:
$\left.\begin{matrix} a // b\\ \widehat{B_1}\, và\, \widehat{E_1} so\,le\,trong\end{matrix}\right\}$ => $\widehat{B_1}$ = $\widehat{E_1}$
$\left.\begin{matrix} a // b\\ \widehat{A_1}\, và\, \widehat{D_1} so\,le\,trong\end{matrix}\right\}$ => $\widehat{A_1}$ = $\widehat{D_1}$
$\widehat{C_1}$ = $\widehat{C_2}$ (hai góc đối đỉnh)
Giải bài 38 trang 95 sgk hình học 7 tập 1
Hãy điền vào chỗ trống (...):Hình 25a
- Biết d // d' thì suy ra:
a) $\widehat{A_1}$ = $\widehat{B_3}$ b) ... c) ...
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) ...
b) ...
c) ...
Hình 25b
- Biết:
a) $\widehat{A_4}$ = $\widehat{B_2}$ hoặc b) ... hoặc c) ...
thì suy ra d // d'
- Nếu một đường thẳng cắt hai đường thẳng mà a) ... hoặc b) ... hoặc c) ... thì hai đường thẳng đó song song với nhau.
Bài giải:
Hình 25a
a) $\widehat{A_1}$ = $\widehat{B_3}$
b) $\widehat{A_2}$ = $\widehat{B_2}$
c) $\widehat{A_1}$ + $\widehat{B_2}$ = $180^0$
- Nếu một đường thẳng cắt hai đường thẳng song song thì:
a) Hai góc so le trong bằng nhau
b) Hai góc đồng vị bằng nhau
c) Hai góc trong cùng phía bù nhau
Hình 25b
- Biết:
a) $\widehat{A_4}$ = $\widehat{B_2}$
hoặc b) $\widehat{A_3}$ = $\widehat{B_3}$
hoặc c) $\widehat{A_4}$ + $\widehat{B_3}$ = $180^0$
thì suy ra d // d'
- Nếu một đường thẳng cắt hai đường thẳng mà
a) Hai góc so le trong bằng nhau
hoặc b) Hai góc đồng vị bằng nhau
hoặc c) Hai góc trong cùng phía bù nhau
thì hai đường thẳng đó song song với nhau.
Giải bài 39 trang 95 sgk hình học 7 tập 1
Đố. Hình 26 cho biết$d_1$ // $d_2$ và một góc tù tại đỉnh A bằng $150^0$Tính góc nhọn tạo bởi a và $d_2$
Gợi ý: Tính số đo của một góc nhọn đỉnh A.
Bài giải:
Kéo dài đường thẳng a cắt $d_2$ tại B. Khi đó đường thẳng a tạo với $d_2$ một góc nhọn $\widehat{B_1}$
Ta có $A_1$ và $A_2$ là hai góc kề bù nên:
$A_1$ + $A_2$ = $180^0$
<=> $A_1$ + $150^0$ = $180^0$
<=> $A_1$ = $180^0$ - $150^0$ = $30^0$
Ta cũng có:
$\left.\begin{matrix} d_1 // d_2\\ \widehat{A_1}\, và\, \widehat{B_1} so\,le\,trong\end{matrix}\right\}$ => $\widehat{A_1}$ = $\widehat{B_1}$ = $30^0$
Vậy góc nhọn tạo bởi a và $d_2$ là $\widehat{B_1}$ = $30^0$





EmoticonEmoticon