Đường thẳng song song với một đường thẳng cho trước.
Giả sử ta có một loạt các điểm cách đều một đường thẳng cho trước, hẳn các điểm đó phải có một tính chất gì đó khá đặc biệt. Sự úp mở của cô giáo trong tiết học trước khiến ta tò mò muốn khám phá. Và sau đây là những gì mà cô giáo muốn ta tìm hiểu, để chuẩn bị cho bài học về đường thẳng song song với một đường thẳng cho trước.
Tứ giác ABKH có:
AB // HK
AH // BK (cùng vuông góc với b)
=> ABKH là hình bình hành
Ta lại có ˆH = 900 (gt)
=> ABKH là hình chữ nhật (theo dấu hiệu nhận biết hình chữ nhật)
=> AH = BK (theo tính chất hình chữ nhật)
Vậy BK = h
Quan sát hình 93, ta nhận thấy:
AH ⊥ b và AH = h => A cách đường thẳng b một khoảng bằng h.
BK ⊥ b và BK = h => B cách đường thẳng b một khoảng bằng h.
Như vậy, mọi điểm thuộc đường thẳng a đều cách đường thẳng b một khoảng bằng h.
Cũng trên hình 93, ta có a // b, AH ⊥ b => AH ⊥ a. Điều đó cho thấy mọi điểm thuộc đường thẳng b cũng cách đường thẳng a một khoảng là h. Ta nói h là khoảng cách giữa hai đường thẳng song song a và b. Vậy thế nào là khoảng cách giữa hai đường thẳng song song? Ta có định nghĩa như sau:
Ta có AH // KM (vì cùng vuông góc với b)
và AH = KM (vì cùng = h)
=> Tứ giác AMKH là hình bình hành.
Ta lại có ˆH = 900 (gt)
Nên AMKH là hình chữ nhật.
=> AM // b
Khi đó theo tiên đề Ơ-clit, điểm M ∈ a
Chứng minh tương tự, ta được M' ∈ a'
Ta có tính chất các điểm cách đều một đường thẳng cho trước.:
Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
Điều đó có nghĩa là:
- Bất kỳ điểm nào nằm trên hai đường thẳng a và a' cũng cách đường thẳng b một khoảng bằng h.
- Ngược lại, bất kỳ điểm nào cách b một khoảng bằng h thì cũng nằm trên đường thẳng a hoặc a'.
Chứng minh bài toán ?4 sgk:
a) Hình thang AEGC có:
AB = BC (gt)
AE // BF // GC (gt)
Theo định lí đường trung bình của hình thang, suy ra EF = FG (1)
Tương tự hình thang BFHD có:
BC = CD (gt)
BF // CG // DH (gt)
Suy ra FG = GH (2) (định lí đường trung bình của hình thang)
Từ (1) và (2) suy ra EF = FG = GH
b) Chứng minh tương tự
Từ bài toán trên, người ta rút ra định lí:
Bài học đã kết thúc, yêu cầu đặt ra với ta là phải nhận biết được khái niệm khoảng cách giữa hai đường thẳng song song, định lí về các đường thẳng song song cách đều, tính chất của các điểm cách đường thẳng cho trước một khoảng cho trước.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!
Khoảng cách giữa hai đường thẳng song song.
Cho hình 93. Tính BK theo h. |
| Hình 93. |
AB // HK
AH // BK (cùng vuông góc với b)
=> ABKH là hình bình hành
Ta lại có ˆH = 900 (gt)
=> ABKH là hình chữ nhật (theo dấu hiệu nhận biết hình chữ nhật)
=> AH = BK (theo tính chất hình chữ nhật)
Vậy BK = h
Quan sát hình 93, ta nhận thấy:
AH ⊥ b và AH = h => A cách đường thẳng b một khoảng bằng h.
BK ⊥ b và BK = h => B cách đường thẳng b một khoảng bằng h.
Như vậy, mọi điểm thuộc đường thẳng a đều cách đường thẳng b một khoảng bằng h.
Cũng trên hình 93, ta có a // b, AH ⊥ b => AH ⊥ a. Điều đó cho thấy mọi điểm thuộc đường thẳng b cũng cách đường thẳng a một khoảng là h. Ta nói h là khoảng cách giữa hai đường thẳng song song a và b. Vậy thế nào là khoảng cách giữa hai đường thẳng song song? Ta có định nghĩa như sau:
Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.
Tính chất của các điểm cách đều một đường thẳng cho trước.
Trước hết ta chứng minh bài toán ?2: |
| Hình 94. |
và AH = KM (vì cùng = h)
=> Tứ giác AMKH là hình bình hành.
Ta lại có ˆH = 900 (gt)
Nên AMKH là hình chữ nhật.
=> AM // b
Khi đó theo tiên đề Ơ-clit, điểm M ∈ a
Chứng minh tương tự, ta được M' ∈ a'
Ta có tính chất các điểm cách đều một đường thẳng cho trước.:
Các điểm cách đường thẳng b một khoảng bằng h nằm trên hai đường thẳng a và a' song song với b và cách b một khoảng bằng h.Từ định nghĩa khoảng cách giữa hai đường thẳng song song và tính chất của các điểm cách đều một đường thẳng cho trước, ta có nhận xét sau:
Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
Điều đó có nghĩa là:
- Bất kỳ điểm nào nằm trên hai đường thẳng a và a' cũng cách đường thẳng b một khoảng bằng h.
- Ngược lại, bất kỳ điểm nào cách b một khoảng bằng h thì cũng nằm trên đường thẳng a hoặc a'.
Đường thẳng song song cách đều.
Trên hình 96, các đường thẳng a, b, c, d song song với nhau và khoảng cách giữa các đường thẳng a và b, b và c, c và d bằng nhau. Ta nói a, b, c, d là những đường thẳng song song cách đều.Chứng minh bài toán ?4 sgk:
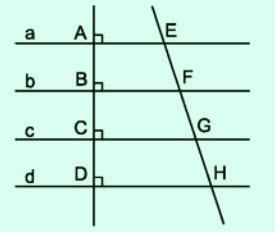 |
| Hình 96. |
AB = BC (gt)
AE // BF // GC (gt)
Theo định lí đường trung bình của hình thang, suy ra EF = FG (1)
Tương tự hình thang BFHD có:
BC = CD (gt)
BF // CG // DH (gt)
Suy ra FG = GH (2) (định lí đường trung bình của hình thang)
Từ (1) và (2) suy ra EF = FG = GH
b) Chứng minh tương tự
Từ bài toán trên, người ta rút ra định lí:
- Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau.Một điều dễ nhận thấy là các định lí về đường trung bình của tam giác, đường trung bình của hình thang là các trường hợp đặc biệt của định lí về các đường thẳng song song cách đều.
- Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
Bài học đã kết thúc, yêu cầu đặt ra với ta là phải nhận biết được khái niệm khoảng cách giữa hai đường thẳng song song, định lí về các đường thẳng song song cách đều, tính chất của các điểm cách đường thẳng cho trước một khoảng cho trước.
Mỗi bài toán có nhiều cách giải, đừng quên chia sẻ cách giải hoặc ý kiến đóng góp của bạn ở khung nhận xét bên dưới. Xin cảm ơn!







EmoticonEmoticon